BÀI 1: Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh BC.a) Chứng minh: Tam giác ABM tam giác ACM.b) Từ M vẽ MH vuông góc AB và MK vuông góc AC.Chứng minh: BH CK.c) Từ B vẽ BP vuông góc AC, BP cắt MH tại I.Chứng minh: Tam giác IBM cân.BÀI 2: Cho tam giác ABC vuông tại A, có AB 4cm, BC 5cm.a) Tính độ dài cạnh AC.b) Tia phân giác của góc ABC cắt AC tại D. Kẻ DE vuông góc BC, tia ED cắt tia BA tại F.Chứng minh: DC DF.c) Chứng minh: AE song s...
Đọc tiếp
BÀI 1: Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh BC.
a) Chứng minh: Tam giác ABM = tam giác ACM.
b) Từ M vẽ MH vuông góc AB và MK vuông góc AC.
Chứng minh: BH = CK.
c) Từ B vẽ BP vuông góc AC, BP cắt MH tại I.
Chứng minh: Tam giác IBM cân.
BÀI 2: Cho tam giác ABC vuông tại A, có AB = 4cm, BC = 5cm.
a) Tính độ dài cạnh AC.
b) Tia phân giác của góc ABC cắt AC tại D. Kẻ DE vuông góc BC, tia ED cắt tia BA tại F.
Chứng minh: DC = DF.
c) Chứng minh: AE song song FC. ( AE // FC )
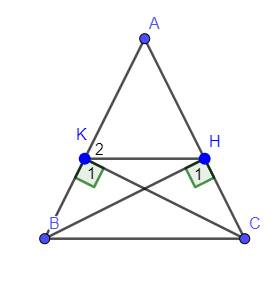
BÀI 3: Cho tam giác ABC cân tại A. ( A^ < 90* ), vẽ BD vuông góc AC và CE vuông góc AB. Gọi H là giao điểm của BD và CE.
a) Chứng minh: Tam giác ABD = tam giác ACE.
b) Chứng minh: Tam giác AED cân.
c) Chứng minh: AH là đường trung trực của ED.
b) Trên tia đối của tia DB lấy điểm K sao cho DK = DB.
Chứng minh: ECB^ = DKC^.
#helpme
#mainopbai