Bài 1.Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:
a) AC P EF. b) Điểm E đối xứng với điểm F qua điểm B
Bài 1.Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:
a) AC P EF. b) Điểm E đối xứng với điểm F qua điểm B
Cho hình bình hành . Điểm đối xứng với điểm qua điểm , điểm đối xứng với điểm qua điểm , điểm đối xứng với điểm qua . Nhận định nào dưới đây đúng?
A. Điểm đối xứng với điểm qua . B. là tâm đối xứng của hình .
C. là hình bình hành. D. Tất cả đáp án trên.
Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(x_0;y_0\right)\) :
a) Tìm tọa độ của điểm A đối xứng với M qua trục Ox
b) Tìm tọa độ của điểm B đối xứng với M qua trục Oy
c) Tìm tọa độ điểm C đối xứng với M qua gốc O
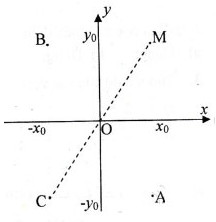
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)
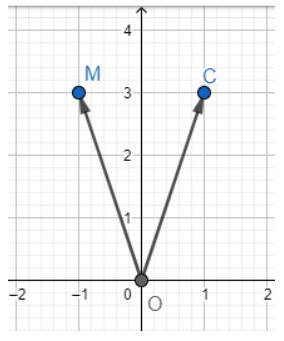
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
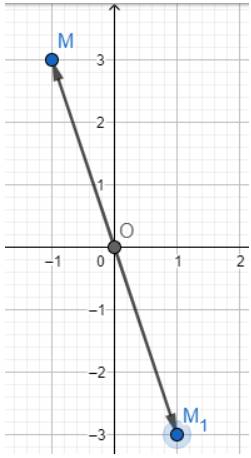
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)

c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(4;3\right)\). Tìm tọa độ của các điểm A, B, C trong các trường hợp sau :
a) A đối xứng với M qua trục Ox
b) A đối xứng với M qua trục Oy
c) C đối xứng với M qua gốc O
a) Hai điểm đối xứng nhau qua trục Ox sẽ có cùng hoành độ và tung độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(4;-3\right)\).
b) Hai điểm đối xứng qua trục Oy sẽ có cùng tung độ và hoành độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(-4;3\right)\).
c) \(A\left(x,y\right)\) có điểm A' đối xứng qua gốc O thì \(A'\left(x';y'\right)\).
\(M\left(4;3\right)\Rightarrow C\left(-4;-3\right)\).
Cho điểm A ( 2;1) . Xác định tọa độ các điểm :
a) B đối xứng với A qua trục tung b) C đối xứng với A qua trục hoành
c) D dối xứng với A qua O d) E đối xứng với A qua đường thẳng d: y = 2x - 1
a: B đối xứng A qua trục tung Oy
=>\(\left\{{}\begin{matrix}x_B=-x_A=-2\\y_B=y_A=1\end{matrix}\right.\)
Vậy: B(-2;1)
b: C đối xứng A qua trục Ox
=>\(\left\{{}\begin{matrix}x_C=x_A=2\\y_C=-y_A=-1\end{matrix}\right.\)
Vậy: C(2;-1)
c: D đối xứng A qua O
=>O là trung điểm của AD
=>\(\left\{{}\begin{matrix}x_A+x_D=0\\y_A+y_D=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=-x_A=-2\\y_D=-y_A=-1\end{matrix}\right.\)
Vậy: D(-2;-1)
d: (d): y=2x-1
=>(d): 2x-y-1=0
E đối xứng A qua (d)
=>(d) là đường trung trực của AD
Gọi (d2): ax+by+c=0 là phương trình đường thẳng AD
(d) là trung trực của AD
=>(d) vuông góc (d2) tại trung điểm của AD(1) và (d2) đi qua A(2;1)
(d): 2x-y-1=0
=>(d2): x+2y+c=0
Thay x=2 và y=1 vào (d2), ta được:
\(c+2+2\cdot1=0\)
=>c=-4
=>(d2): x+2y-4=0
Tọa độ giao điểm F của (d) với (d2) là:
\(\left\{{}\begin{matrix}x+2y-4=0\\2x-y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=8\\2x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=7\\x+2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{7}{5}\\x=4-2y=4-\dfrac{14}{5}=\dfrac{6}{5}\end{matrix}\right.\)
(1) suy ra F là trung điểm của AE
=>\(\left\{{}\begin{matrix}\dfrac{6}{5}=\dfrac{x_A+x_E}{2}=\dfrac{2+x_E}{2}\\\dfrac{7}{5}=\dfrac{y_A+y_E}{2}=\dfrac{y_E+1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_E+2=\dfrac{12}{5}\\y_E+1=\dfrac{14}{5}\end{matrix}\right.\Leftrightarrow E\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AC, AB. Gọi O là 1 điểm bất kì. A' là điểm đối xứng với O qua D, B' là điểm đối xứng với O qua E, C' là điểm đối xứng với O qua F. Chứng minh AA', BB', CC' đồng quy tại 1 điểm.
 Võ Hồng Nhung
Võ Hồng Nhung
1 phút trước (15:05)
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AC, AB. Gọi O là 1 điểm bất kì. A' là điểm đối xứng với O qua D, B' là điểm đối xứng với O qua E, C' là điểm đối xứng với O qua F. Chứng minh AA', BB', CC' đồng quy tại 1 điểm.
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ
a) Điểm H là hình chiếu vuông góc của M trên trục Ox
b) Điểm M’ đối xứng với M qua trục Ox
c) Điểm K là hình chiếu vuông góc của M trên trục Oy
d) Điểm M’’ đối xứng với M qua trục Oy
e) Điểm C đối xứng với M qua gốc tọa độ
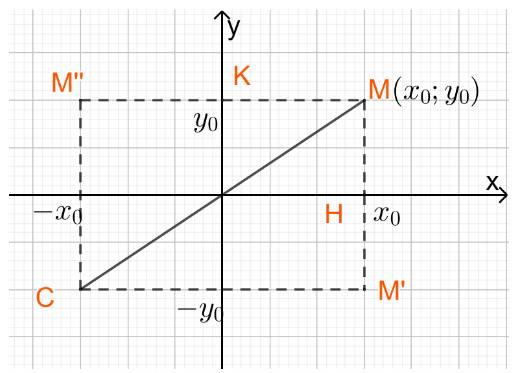
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)
Cho góc vuông xOy, điểm A trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O ?
54. Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng mình rằng điểm B đối xứng với điểm C qua O.
Bài giải:
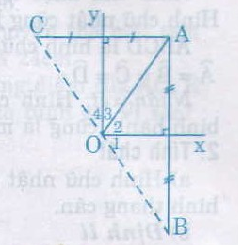
Cách 1:
B đối xứng với A qua Ox nên Ox là đường trung trực của AB => OA = OB
C đối xứng với A qua Oy nên OY là đường trung trực của AC => OA = OC
Suy ra OB = OC (1)
∆AOB cân tại O =>ˆO1O1^ = ˆO2O2^ = ˆAOB2AOB2^
∆AOC cân tại O =>ˆO3O3^ = ˆO4O4^ = ˆAOC2AOC2^ˆAOBAOB^ˆAOCAOC^
Mà widehatAOBwidehatAOB + ˆAOCAOC^ = 2(ˆO2O2^ + ˆO3O3^) = 2.900 = 1800
=> B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
Cách 2:
A đối xứng với B qua Ox và O nằm trên Ox nên OA đối xứng với OB qua OX suy ra
OA = OB.
A đối xứng với C qua Oy và O nằm trren Oy nên OA đối xứng với OC qua Oy.
Suy ra OA = OC
Do đó OB = OC (1)
và ˆAOBAOB^ + ˆAOCAOC^ = 2(ˆO2O2^ + ˆO3O3^) = 2.900 = 1800
=>B, O, C thẳng hàng (2)
Từ (1) và (2) suy ra B đối xứng với C qua O.
Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy. Chứng minh rằng điểm B đối xứng với điểm C qua O.
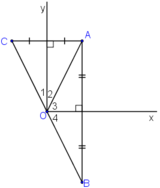
+ B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
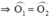
Xét ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
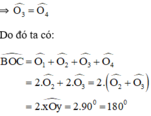
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
⇒ B đối xứng với C qua O.