Có ai ko giúp mik voi mik cần gấp .cảm ơn
BD
Những câu hỏi liên quan
ai đó có tâm giúp mik vs, ảnh trên này nó ko chịu tải ạ. Mà mik cần người chỉ gấp lắm r ạ:((. Bạn nào giúp đc thì liên hệ zalo:0797136882, mik gửi hình cho,cảm ơn nhiều
Mn ai có một số dạng bài về viết lại câu nhưng nghĩa ko đổi ở lớp 7 ko , mik cần gấp mik cảm ơn trước![]()
Help mik với pl mik xin cảm tạ ai giúp bài 2 nha mik cần gấp lắm ko có nó mik mất đt xin cacsc bạn giúp mik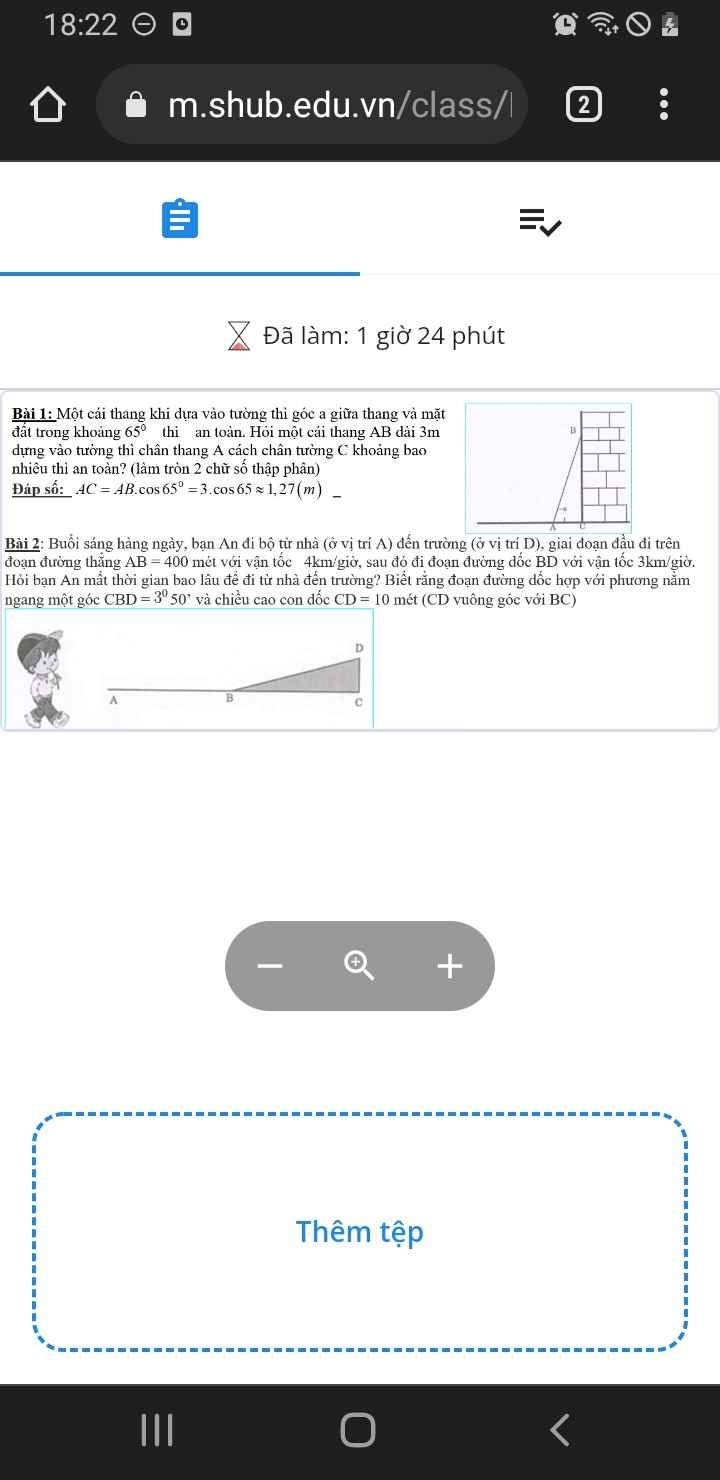
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)
Đúng 0
Bình luận (0)

Ai giúp mik với mik cảm ơn mik đang cần gấp lắm ạ
c: \(=\dfrac{-27\cdot100}{-30}=\dfrac{2700}{30}=90\)
Đúng 2
Bình luận (0)
mng giúp mik bài này được ko? mik đang cần gấp . cảm ơn bạn nhiều 
a: =>x>=0 và x^2+x=x^2
=>x=0
a: =>x>=1 và 1-x^2=x^2-2x+1
=>-2x^2+2x=0 và x>=1
=>x=1
a: =>x>=1 và 1-2x^2=x^2-2x+1
=>-3x^2+2x=0 và x>=1
=>\(x\in\varnothing\)
a: ĐKXĐ: x<=2 và x^2-2x=x^2-4x+4
=>x=2
a: =>căn x^2-4=x-2
=>x>=2 và x^2-4=x^2-4x+4
=>x>=2 và 4x=8
=>x=2
b: =>x>=0 và x^2-4x+1=x^2
=>-4x+1=0 và x>=0
=>x=1/4
b: =>x>=-1 và x^2+x+1=x^2+2x+1
=>x=0
c: =>x>=1 và 4x^2-8x+1=x^2-2x+1
=>x>=1 và 3x^2-6x=0
=>x=2
b: =>x>=-1 và 5x^2-2x+2=x^2+2x+1
=>x>=-1 và 4x^2-4x+1=0
=>x=1/2
b: =>căn 4x^2-x+1=2x+3
=>x>=-3/2 và 4x^2-x+1=(2x+3)^2=4x^2+12x+9
=>x>=-3/2 và -13x=8
=>x=-8/13
Đúng 1
Bình luận (2)
1) \(\sqrt{x^2+x}=x\) (Thỏa mẵn với mọi x)
\(\Leftrightarrow x^2+x=x^2\)
\(\Leftrightarrow x^2+x-x^2=0\)
\(\Leftrightarrow x=0\)
Vậy \(x=0\)
2) \(\sqrt{1-x^2}=x-1\) (ĐK: \(x\le1\) )
\(\Leftrightarrow1-x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-x^2=x^2-2x+1\)
\(\Leftrightarrow-x^2-x^2+2x=1-1\)
\(\Leftrightarrow-2x^2+2x=0\)
\(\Leftrightarrow-2x\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;1\right\}\)
\(\sqrt{1-2x^2}=x-1\) (ĐK: \(x\le\sqrt{\dfrac{1}{2}}\))
\(\Leftrightarrow1-2x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-2x^2=x^2-2x+1\)
\(\Leftrightarrow-2x^2-x^2+2x=1-1\)
\(\Leftrightarrow-3x^2+2x=0\)
\(\Leftrightarrow-x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{2}{3}\right\}\)
\(\sqrt{x^2-2x}=2-x\) (ĐK: \(\left\{{}\begin{matrix}x\le0\\x\ge2\end{matrix}\right.\) )
\(\Leftrightarrow x^2-2x=\left(2-x\right)^2\)
\(\Leftrightarrow x^2-2x=4-4x+x^2\)
\(\Leftrightarrow x^2-x^2-2x+4x=4\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
\(\sqrt{x^2-4}-x+2=0\) (ĐK: \(\left\{{}\begin{matrix}x\le-2\\x\ge2\end{matrix}\right.\))
\(\Leftrightarrow\sqrt{x^2-4}=x-2\)
\(\Leftrightarrow x^2-4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2+4x=4+4\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
Đúng 1
Bình luận (0)

Ai lm giúp mik vs...Mik đang cần gấp ạ ( Cảm ơn )
\(a,\dfrac{11x}{2x-5}+\dfrac{x-30}{2x-5}=\dfrac{11x+x-30}{2x-5}=\dfrac{12x-30}{2x-5}=\dfrac{6\left(2x-5\right)}{2x-5}=6\)
\(b,\dfrac{3x^2-1}{2x}+\dfrac{x^2+1}{2x}=\dfrac{3x^2-1+x^2+1}{2x}=\dfrac{4x^2}{2x}=2x\)
\(c,\dfrac{3}{2x-5}+\dfrac{-2}{2x+5}+\dfrac{-20}{4x^2-25}=\dfrac{3\left(2x+5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{2\left(2x-5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{6x+15-4x+10-20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{1}{2x-5}\)
\(d,\dfrac{x-2}{x-1}+\dfrac{x-3}{x+1}+\dfrac{4-2x^2}{x^2-1}=\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-3\right)\left(x-1\right)+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+x-2+x^2-3x-x+3+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5}{x-1}\)
\(e,\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}+\dfrac{4}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1-x^2+2x-1+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)
Đúng 1
Bình luận (0)
ai giúp mik vs mik đag cần gấp ạ cảm ơn nhiều
Mng giúp mik bài này được ko? Mik đang cần gấp. Cảm ơn bạn nhiều 🤩
mng giúp mik 2 câu này đực ko, mik đang cần gấp. Cảm ơn bạn nhiều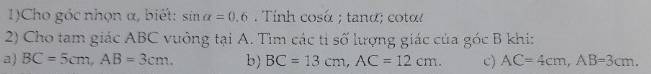
2:
a: AC=căn 5^2-3^2=4cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
b: AB=căn 13^2-12^2=5cm
sin B=AC/BC=12/13
cos B=AB/BC=5/13
tan B=12/13:5/13=12/5
cot C=1:12/5=5/12
c: BC=căn 4^2+3^2=5cm
sin B=AC/BC=4/5
cos B=AB/BC=3/5
tan B=4/5:3/5=4/3
cot B=1:4/3=3/4
Đúng 1
Bình luận (0)










