rút gọn
√(2a/3)*√(3a/8) với a>=0
√5*√45a-3a với a>=0
Bài 20 (trang 15 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $\sqrt{\dfrac{2a}{3}}.\sqrt{\dfrac{3a}{8}}$ với $a\ge 0$ ; b) $\sqrt{13a}.\sqrt{\dfrac{52}{a}}$ với $a>0$ ;
c) $\sqrt{5a}.\sqrt{45a}-3a$ với $a\ge 0$ ; d) $(3-a)^2-\sqrt{0,2}.\sqrt{180a^2}$.
a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)
a) Ta có:
b) Ta có:
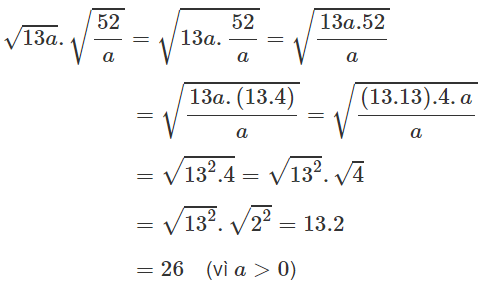
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:
d) Ta có:
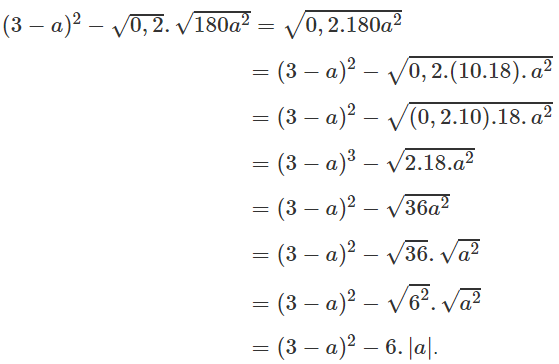
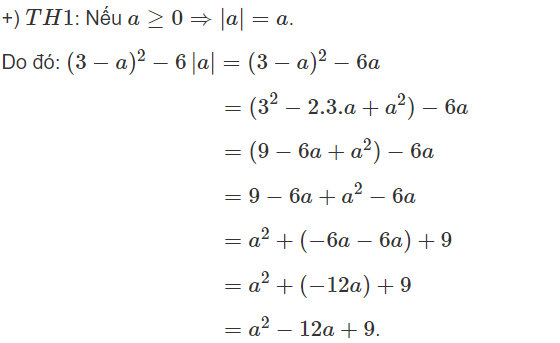
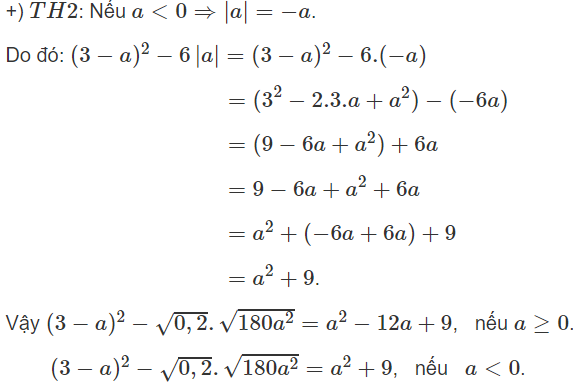
b) \(\sqrt{13a}\).\(\sqrt{\frac{52}{a}}\)=\(\sqrt{13a.\frac{52}{a}}\)=\(\sqrt{13.13.2.2}\)=13.2=26
3a+1/3 x √27/9 1+ 3a)^2 với a > -1/3
rút gọn zùm mình với
a \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
b \(\sqrt{\dfrac{2a}{3}}.\sqrt{\dfrac{3a}{8}}\) với a>0
c \(\sqrt{5a.45a}-3a\) với a<0
a: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{4}+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=1+\sqrt{2}\)
b: \(\sqrt{\dfrac{2a}{3}}\cdot\sqrt{\dfrac{3a}{8}}=\sqrt{\dfrac{6a^2}{24}}=\sqrt{\dfrac{a^2}{4}}=\dfrac{a}{2}\)
c: \(\sqrt{5a\cdot45a}-3a=-15a-3a=-18a\)
Cho biểu thức: \(A=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
Với x≠±2,x≠0,x≠3
a, Rút gọn biểu thức A
b,Tính giá trị của A khi x=12
c, Tính x khi A=1
d, Tìm x∈Z để A nguyên
e, Tìm x để biểu thức A>4
Lời giải:
a.
\(A=\left[\frac{(2+x)^2}{(2-x)(2+x)}+\frac{4x^2}{(2-x)(2+x)}-\frac{(2-x)^2}{(2-x)(2+x)}\right]:\frac{x(x-3)}{x^2(2-x)}\)
\(=\frac{(2+x)^2+4x^2-(2-x)^2}{(2-x)(2+x)}.\frac{x^2(2-x)}{x(x-3)}=\frac{4x(x+2)}{(2-x)(2+x)}.\frac{x^2(2-x)}{x(x-3)}=\frac{4x^2}{x-3}\)
b.
Khi $x=12$ thì $A=\frac{4.12^2}{12-3}=64$
c.
$A=1\Leftrightarrow \frac{4x^2}{x-3}=1$
$\Leftrightarrow 4x^2=x-3$
$\Leftrightarrow 4x^2-x+3=0$
$\Leftrightarrow (2x-\frac{1}{4})^2=-\frac{47}{16}< 0$ (vô lý)
Vậy không tồn tại $x$
d. Để $A$ nguyên thì $\frac{4x^2}{x-3}$ nguyên
$\Leftrightarrow 4x^2\vdots x-3$
$\Leftrightarrow 4(x^2-9)+36\vdots x-3$
$\Leftrightarrow 36\vdots x-3$
$\Leftrightarrow x-3\in\left\{\pm 1;\pm 2;\pm 3;\pm 4;\pm 9; \pm 12; \pm 36\right\}$
Đến đây bạn có thể tự tìm $x$ được rồi, chú ý ĐKXĐ để loại ra những giá trị không thỏa mãn.
e.
$A>4\Leftrightarrow \frac{4x^2}{x-3}>4$
$\Leftrightarrow \frac{x^2}{x-3}>1$
$\Leftrightarrow \frac{x^2-x+3}{x-3}>0$
$\Leftrightarrow x-3>0$ (do $x^2-x+3>0$ với mọi $x$ thuộc ĐKXĐ)
$\Leftrightarrow x>3$. Kết hợp với đkxđ suy ra $x>3$
Bài 5: ( 1 điểm )
a) Rút gọn biểu thức : B = \(\dfrac{2a-b}{3a-b}+\dfrac{5b-a}{3a+b}-3\)
b) Tính giá trị của biểu thức B biết: 10a2 - 3b2 - 5ab = 0 & 9a2 - b2 ≠ 0
Rút gọn : \(\left(\frac{1+2a}{4+2a}-\frac{a}{3a-6}+\frac{2a^2}{12-3a^2}\right)\div\frac{13a+6}{24-12a}\)
\(=\left(\dfrac{2a+1}{2\left(a+2\right)}-\dfrac{a}{3\left(a-2\right)}-\dfrac{2a^2}{3\left(a-2\right)\left(a+2\right)}\right):\dfrac{13a+6}{24-12a}\)
\(=\dfrac{3\left(2a+1\right)\left(a-2\right)-2a\left(a+2\right)-4a^2}{6\left(a-2\right)\left(a+2\right)}:\dfrac{13a+6}{-12\left(a-2\right)}\)
\(=\dfrac{3\left(2a^2-3a-2\right)-2a\left(a+2\right)-4a^2}{6\left(a-2\right)\left(a+2\right)}\cdot\dfrac{-12\left(a-2\right)}{13a+6}\)
\(=\dfrac{6a^2-9a-6-2a^2-4a-4a^2}{a+2}\cdot\dfrac{-2}{13a+6}\)
\(=\dfrac{-\left(13a+6\right)}{a+2}\cdot\dfrac{-2}{13a+6}=\dfrac{2}{a+2}\)
Cho Q=\(\dfrac{a^3-3a^2+3a-1}{a^2-1}\)
a,Rút gọn Q
b,Tìm giá trị của Q khi |a|=5
`Q=(a^3-3a^2+3a-1)/(a^2-1)`
`a)ĐK:a^2-1 ne 0<=>a ne +-1`
`Q=(a^3-3a^2+3a-1)/(a^2-1)`
`=(a-1)^3/((a-1)(a+1))`
`=(a-1)^2/(a+1)`
`b)|a|=5`
`<=>` \(\left[ \begin{array}{l}a=5\\a=-5\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}Q=\dfrac{(5-1)^2}{5+1}=\dfrac83\\Q=\dfrac{(-5-1)^2}{-5+1}=-9\end{array} \right.\)
1) \(\sqrt{9a^2.b^2}\) với a<0, b<0
2) \(\sqrt{3a}.\sqrt{27a}\) với a \(\ge\)0
3) \(\sqrt{3a^5}.12a\) với a>0
4) \(\sqrt{5a}.\sqrt{45a}-3a\) ( với a ≥ 0)
5) \(\sqrt{3+\sqrt{a}}\).\(\sqrt{3-\sqrt{a}}\)
6) \(\sqrt{3+\sqrt{5}}\). \(\sqrt{3\sqrt{5}}\)
\(1) \sqrt{9a^2.b^2}\)=3ab
\(2) \sqrt{3a}.\sqrt{27a}=\sqrt{3a}.3\sqrt{3a}=9a\)
\(3) \sqrt{3a^5}.12a=12\sqrt{3a^7}\)
\(4) \sqrt{5a}.\sqrt{45a}-3a=15a-3a=12a\)
\(5) \sqrt{3+\sqrt{a}}.\sqrt{3-\sqrt{a}}=\sqrt{(3+\sqrt{a}).(3-\sqrt{a})} =\sqrt{9-a} \)
\(6) \sqrt{3+\sqrt{5}}.\sqrt{3\sqrt{5}} =\sqrt{\sqrt{3\sqrt{5}}.(3+\sqrt{5})} =\sqrt{9+\sqrt{15}}\)
1) \(\sqrt{9a^2b^2}=3ab\)
2) \(\sqrt{3a}\cdot\sqrt{27a}=9a\)
4) \(\sqrt{5a}\cdot\sqrt{45a}-3a=15a-3a=12a\)
Bài 1 : Cho phương trình ẩn x :
x-a / x+a - x+a/x-a + 3a^2+a/x^2-a^2 = 0
a) Giải phương trình với a = -3
b) Giải phương trình với a = 1
c) Xác định a để phương trình có nghiệm x = 0,5
Bài 2 : Với giá trị nào của a để biểu thức a có giá trị = 2
a) 2a-9/2a-5 + 3a/3a-2
b) 3a+2/3a+4 + a-2/a-4
Bài 3 : Giải phương trình :
a) x+5/x-1 = x+1/x-3 - 8/x^2-4x+3
b) x+1/x^2+x+1 - x-1/x^2-x+1 = 3/x(x^4+x^2+1)
Các bạn ĐT Toán xinh gái , đẹp trai bơi vào đây giúp mk vs
Cảm ơn trước nha
Xog mk tik cho
♥♥♥♥♥♥
tìm ra đáp án chưa
Đc rồi chỉ mình với
Bài 3:
a: \(\Leftrightarrow\left(x+5\right)\left(x-3\right)=\left(x+1\right)\left(x-1\right)-8\)
\(\Leftrightarrow x^2+2x-15=x^2-1-8=x^2-9\)
=>2x=6
hay x=3(loại)
b: \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2-x+1\right)\left(x^2+x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(\Leftrightarrow x\left(x^3+1-x^3+1\right)=3\)
=>2x=3
hay x=3/2