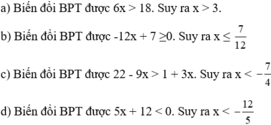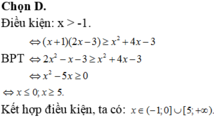(2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x2 – 5

⇔ 2x2 + 6x - x – 3 – 3x + 1 ≤ x2 + 3x - x – 3 + x2 – 5

⇔ 2x2 + 2x – 2 ≤ 2x2 + 2x – 8

⇔ 6 ≤ 0 (Vô lý).

Vậy BPT vô nghiệm.

1.

\(6+2x\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

\(\Leftrightarrow x\ge-1\)

2.

\(2x+7>16-x\)

\(\Leftrightarrow3x>23\)

\(\Leftrightarrow x>\dfrac{23}{3}\)

3.

\(x-5< 3x+1\)

\(\Leftrightarrow2x>-6\)

\(\Leftrightarrow x>-3\)

Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:

1. 6 + 2x \(\ge\) 3 - x

<=> 6 - 3 \(\ge\) -x - 2x

<=> 3 \(\ge\) -3x

<=> 3 : (-3) \(\ge\) -3x : (-3)

<=> -1 \(\le\) x

<=> x \(\ge\) -1

2. 2x + 7 > 16 - x

<=> 2x + x > 16 - 7

<=> 3x > 9

<=> 3x : 3 > 9 : 3

<=> x > 3

3. x - 5 < 3x + 1

<=> -5 - 1 < 3x - x

<=> -6 < 2x

<=> -6 : 2 < 2x : 2

<=> -3 < x

<=> x > (-3)

1: Ta có: \(2x+6\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

hay \(x\ge-1\)

2: ta có: \(2x+7>16-x\)

\(\Leftrightarrow3x>9\)

hay x>3

3: Ta có: \(x-5< 3x+1\)

\(\Leftrightarrow-2x< 6\)

hay x>-3

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)

\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)

Bảng xét dấu:

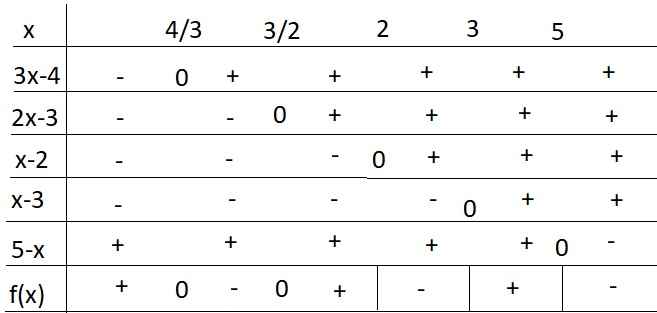
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2

(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)

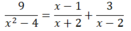
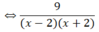
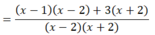
Vậy tập nghiệm của pt là: S = {-1; 1}

b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0

Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x

⇔ x = -5 hoặc x = 5/3

Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}

c) x – 2)2 + 2(x – 1) ≤ x2 + 4

⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4

⇔ -2x ≤ 2

⇔ x ≥ -1

Tập nghiệm S = {x | x ≥ -1}

Bài 1: 

a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)

\(\Leftrightarrow6-8x-10+2x-5=0\)

\(\Leftrightarrow-6x+11=0\)

\(\Leftrightarrow-6x=-11\)

hay \(x=\dfrac{11}{6}\)

b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)

\(\Leftrightarrow6-12x-11+3x-1=0\)

\(\Leftrightarrow-9x-6=0\)

\(\Leftrightarrow-9x=6\)

hay \(x=-\dfrac{2}{3}\)

a, \(\dfrac{x+1}{x+3}>1\Leftrightarrow\dfrac{x+1}{x+3}-1>0\Leftrightarrow\dfrac{x+1-x-3}{x+3}>0\)

\(\Rightarrow x+3< 0\)do  -2 < 0 

\(\Rightarrow x< -3\)Vậy tập nghiệm BFT là S = { x | x < -3 } 

b, \(\dfrac{2x-1}{x-3}\le2\Leftrightarrow\dfrac{2x-1}{x-3}-2\le0\Leftrightarrow\dfrac{2x-1-2x+6}{x-3}\le0\)

\(\Rightarrow x-3\le0\)do 5 > 0 

\(\Rightarrow x\le3\)Vậy tập nghiệm BFT là S = { x | x \(\le\)3 } 

c, \(\dfrac{x^2+2x+2}{x^2+3}\ge1\Leftrightarrow\dfrac{x^2+2x+2}{x^2+3}-1\ge0\)

\(\Leftrightarrow\dfrac{x^2+2x+2-x^2-3}{x^2+3}\ge0\Rightarrow2x-1\ge0\)do x^2 + 3 > 0 

\(\Rightarrow x\ge\dfrac{1}{2}\)Vậy tập nghiệm BFT là S = { x | x \(\ge\)1/2 } 

mình ko chắc nên mình đăng sau :> 

d, \(\dfrac{2x+1}{x^2+2}\ge1\Leftrightarrow\dfrac{2x+1}{x^2+2}-1\ge0\Leftrightarrow\dfrac{2x+1-x^2-2}{x^2+2}\ge0\)

\(\Rightarrow-x^2+2x-1\ge0\Rightarrow-\left(x-1\right)^2\ge0\)vô lí 

Lời giải:

PT $\Leftrightarrow (x^2-1)^3+(x^2+2)^3+(2x-1)^3-3(x^2-1)(x^2+2)(2x-1)=0$

Đặt $x^2-1=a; x^2+2=b; 2x-1=c$ thì pt trở thành:
$a^3+b^3+c^3-3abc=0$

$\Leftrightarrow (a+b)^3+c^3-3ab(a+b)-3abc=0$

$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$

$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$

$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$

Nếu $a+b+c=0$

$\Leftrightarrow x^2-1+x^2+2+2x-1=0$

$\Leftrightarrow 2x^2+2x=0$

$\Rightarrow x=0$ hoặc $x=-1$
Nếu $a^2+b^2+c^2-ab-bc-ac=0$

$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$

$\Rightarrow a-b=b-c=c-a=0$ (dễ CM)

$\Leftrightarrow a=b=c$

$\Leftrightarrow x^2-1=x^2+2=2x-1$ (vô lý)

Vậy..........