Cho tam giác ABC vuông tại A . Gọi M là d' nằm bên trong của tam giác đó. Chứng minh <BMc là góc tù
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NT
Những câu hỏi liên quan
cho tam giác ABC vuông cân tại A. Gọi D là một điểm nằm trong tam giác sao cho góc DBC= góc DCA=30 độ. Chứng minh rằng tam giác ACD là tam giác cân. Tính góc tam giác cân đó.
đố ai giải được bài toán khó lớp 7 này đấy (em trong đội tuyển hsg toán nè!)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. gọi D là 1 điểm nằm trong tam giác ABC, sao cho góc DBC = góc DCA =30 độ . chứng minh rằng tam giác ACD cân , tính các góc của tam giác ACD
Đề bài thiếu, nếu ABC là tam giác vuông bất kì thì không thể chứng minh ACD là tam giác cân được. ABC phải là tam giác vuông cân.
Câu hỏi này đã có trả lời ở đây: https://olm.vn/hoi-dap/detail/185970928943.html
Đúng 0
Bình luận (0)
Câu hỏi của linh ngoc - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Tam giác ABC vuông cân tại A
Trên cùng nửa mặt phẳng bờ AC chứa B vẽ tam giác đều ACE.
Ta có: \(\widehat{ACE}=60^o\)
=> \(\widehat{BCE}=\widehat{ACE}-\widehat{ACE}=60^o-45^o=15^o\)
và \(\widehat{BCD}=\widehat{BCA}-\widehat{DCA}=45^o-30^o=15^o\)
Suy ra \(\widehat{BCE}=\widehat{BCD}\)(1)
Mặt khác Ta có tam giác ABC vuông cân tại A => AB=AC
Tam giác ACE đều => AE=AC
=> AB=AE => Tam giác BAE cân tại A
mà \(\widehat{BAE}=\widehat{BAC}-\widehat{EAC}=90^o-60^o=30^o\)
=> \(\widehat{ABE}=\widehat{AEB}=\frac{180^o-\widehat{BAE}}{2}=75^o\)
=> \(\widehat{CBE}=\widehat{ABE}-\widehat{ABC}=75^o-45^o=30^o\)
=> \(\widehat{CBE}=\widehat{CBD}\left(=30^o\right)\)(2)
Xét tam giác DBC và tam giác EBC có
\(\widehat{BCE}=\widehat{BCD}\)(1),
\(\widehat{CBE}=\widehat{CBD}\left(=30^o\right)\)theo (2)
và BC chung
=> tam giác DBC=EBC
=> DC=EC=AC
=> Tam giác ADC cân tại C
\(\widehat{ACD}=30^o\Rightarrow\widehat{DAC}=\widehat{ADC}=\frac{180^o-\widehat{ACD}}{2}=75^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh: tam giác MAB = tam giác MDC
b) Chứng minh: AB // CD và tam giác ABC = tam giác CDA
c) Chứng minh: Tam giác BDC vuông tại D
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: AB//CD
AB\(\perp\)AC
Do đó: CD\(\perp\)CA
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AB=CD
AC chung
Do đó: ΔABC=ΔCDA
c: Ta có: ΔABC=ΔCDA
=>BC=DA
Xét ΔMCA và ΔMBD có
MC=MB
\(\widehat{CMA}=\widehat{BMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMCA=ΔMBD
=>\(\widehat{MCA}=\widehat{MBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)CD
Do đó: DC\(\perp\)DB
=>ΔDBC vuông tại D
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc nhọn tại A. Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A là ABD và ACE. Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc với DE.
Cho tam giác ABC vuông cân tại A. Lấy điểm P nằm bên trong tam giác ABC. Dựng tam giác APQ vuông cân tại A sao cho Q và C nằm về hai nửa mặt phẳng đối bờ là AB.a) Chứng minh rằngBQCP.b) Biết góc APB 135. Chứng minh rằng CP2−BP2 2·AP2.
Đọc tiếp
Cho tam giác ABC vuông cân tại A. Lấy điểm P nằm bên trong tam giác ABC. Dựng tam giác APQ vuông cân tại A sao cho Q và C nằm về hai nửa mặt phẳng đối bờ là AB.
a) Chứng minh rằngBQ=CP.
b) Biết góc APB= 135. Chứng minh rằng CP2−BP2= 2·AP2.
Cho tam giác ABC vuông cần tại A. Gõi D là một điểm nằm trong tam giác đó sao cho góc DBC=DCA=30 độ. Chứng minh tam giác ACD là tam giác cân. Tính góc tam giác đó
cho tam giác ABC cân tại A.Trên cạnh BC lấy D,E (D nằm giữa B và E sao cho BD=CE).Vẽ DM vuông góc với AB tại M, EN vuông góc với AC tại N. gọi K là giao điểm của MD và NE. Chứng minh rằng: a) tam giác MBD = tam giác NCE. b) tam giác MAK = tam giác NAK
a: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
DB=EC
\(\widehat{DBM}=\widehat{ECN}\)(ΔABC cân tại A)
Do đó: ΔMBD=ΔNCE
b: Ta có: ΔMBD=ΔNCE
=>MB=NC
Ta có: AM+MB=AB
AN+NC=AC
mà MB=NC và AB=AC
nên AM=AN
Xét ΔAMK vuông tại M và ΔANK vuông tại N có
AK chung
AM=AN
Do đó: ΔAMK=ΔANK
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB =a, AC =b. Tam giác ACD vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
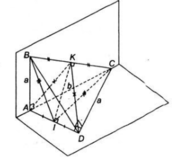


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A .Dựng ở miền ngoài tam giác ABC các hình vuông ABHK,ACDE1.chứng minh H,A,D thẳng hàng 2.đường thẳng HD cắt đường tròn ngoại tiếp tam giác ABC tại F. chứng minh tam giác FBC vuông cân 3. cho biết góc ABC45 độ . gọi M là giao điểm của BF và ED . chứng minh 5 điểm B,K,E,M,C cùng nằm trên một đường tròn4. chứng minh MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
Đọc tiếp
cho tam giác ABC vuông tại A .Dựng ở miền ngoài tam giác ABC các hình vuông ABHK,ACDE
1.chứng minh H,A,D thẳng hàng
2.đường thẳng HD cắt đường tròn ngoại tiếp tam giác ABC tại F. chứng minh tam giác FBC vuông cân
3. cho biết góc ABC>45 độ . gọi M là giao điểm của BF và ED . chứng minh 5 điểm B,K,E,M,C cùng nằm trên một đường tròn
4. chứng minh MC là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
Em tài trợ cái hình cho mọi người dễ nhìn ạ!
Đúng 0
Bình luận (0)
à, cái chỗ đoạn thẳng H, A, D là đường đứt khúc ạ, em quên sửa!
Đúng 0
Bình luận (0)
ý em là: đoạn thẳng nối H, A và D là đường đứt khúc!
Đúng 0
Bình luận (0)



