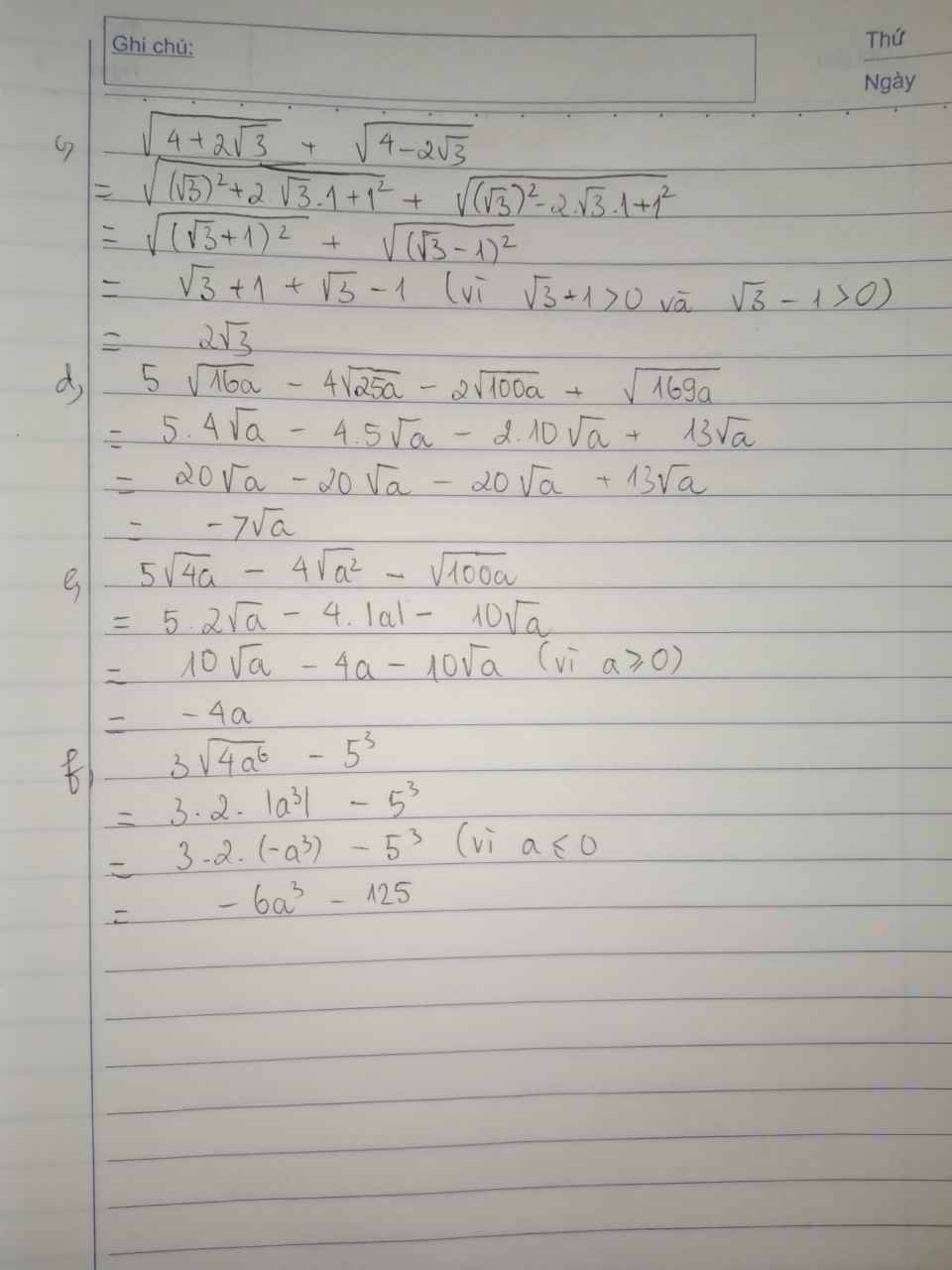\(4a^4-25a^3+16a^2-9\)
TT
Những câu hỏi liên quan
rút gọn các biểu thức sau
c,\(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\) d,\(5\sqrt{16a}-4\sqrt{25a}-2\sqrt{100a}+\sqrt{169a}\) với a ≥ 0
e,\(5\sqrt{4a}-4\sqrt{a^2}-\sqrt{100a}\) với a ≥ 0 f,\(3\sqrt{4a^6}-5^3\) với a ≤ 0
5√16a - 4√25a + √169a
5√16a - 4√25a + √169a
= 5.4a - 4.5a + 13a
= 13a
Đúng 2
Bình luận (0)
Rút gọn biểu thức :
a) 5\(\sqrt{25a^2}-25a\)với a ≤ 0 ;
b) \(\sqrt{16a^4}+6a^2\)
Lời giải:
a)
$5\sqrt{25a^2}-25a=5\sqrt{(5a)^2}-25a=5|5a|-25a$
Với $a\leq 0$ thì $|5a|=-5a$. Do đó:
$5\sqrt{25a^2}-25a=-25a-25a=-50a$
b)
$\sqrt{16a^4}+6a^2=\sqrt{(4a^2)^2}+6a^2=|4a^2|+6a^2=4a^2+6a^2=10a^2$
Đúng 0
Bình luận (0)
Rút gọn biểu thức: P=\(\dfrac{9\sqrt{a}-\sqrt{25a}+\sqrt{4a^3}}{a^2+2a}\)với a>0
\(P=\dfrac{9\sqrt{a}-\sqrt{25a}+\sqrt{4a^3}}{a^2+2a}=\dfrac{9\sqrt{a}-5\sqrt{a}+2a\sqrt{a}}{a\left(a+2\right)}=\dfrac{4\sqrt{a}+2a\sqrt{a}}{a\left(a+2\right)}=\dfrac{2\sqrt{a}\left(2+a\right)}{a\left(2+a\right)}=\dfrac{2\sqrt{a}}{a}=\dfrac{2.\sqrt{a}}{\sqrt{a}.\sqrt{a}}=\dfrac{2}{\sqrt{a}}\)
Đúng 1
Bình luận (0)
√9a + √16a - √25a + √121a
Cho a,b,c \(\in\) N*, thỏa mãn\(\left\{{}\begin{matrix}a+b+c=20\\16a+2b+c=80\end{matrix}\right.\)
Hãy tính giá trị của biểu thức M= 25a-4a-2007c
\(\left\{{}\begin{matrix}a+b+c=20\\16a+2b+c=80\end{matrix}\right.\)\(\) \(\left\{{}\begin{matrix}a+b+c=20\\16a+b=60\end{matrix}\right.\)
\(\left\{{}\begin{matrix}b=60-15a\\c=14a-40\end{matrix}\right.\)
\(\left\{{}\begin{matrix}60-15a>0\Rightarrow a< 4\\14a-40>0\Rightarrow a\ge3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=15\\c=2\end{matrix}\right.\)
Thay vào => M
"mình nghi ngờ biểu thức M của bạn sai"
Đúng 0
Bình luận (0)
\(5\sqrt{25a^2}-25a\) với a<0
\(\sqrt{16a^4}+6a^3\) với a bất kì
\(3\sqrt{9a}^6-6a^3\) với a bất kì
\(4x-\sqrt{x^2-4x+4}\) với x _< (bé hơn hoặc bằng) 2
mọi người giúp em với ạ , em cảm ơn :)
\(\sqrt{4x^2-4x+1}+2=3x\)
Rút gọn
\(7\sqrt{a}-5b\sqrt{16a^3}+4a\sqrt{25ab^2}-3\sqrt{16a}\) với a>0, b>0
\(\sqrt{4x^2-4x+1}+2=3x\)
Vì \(VT\ge2\Rightarrow VP\ge2\Rightarrow x\ge\dfrac{2}{3}\)
\(\Rightarrow\sqrt{\left(2x-1\right)^2}+2=3x\Rightarrow\left|2x-1\right|+2=3x\)
\(\Rightarrow2x-1+2=3x\left(x\ge\dfrac{2}{3}\right)\Rightarrow x=1\)
\(7\sqrt{a}-5b\sqrt{16a^3}+4a\sqrt{25ab^2}-3\sqrt{16a}\)
\(=7\sqrt{a}-20ab\sqrt{a}+20ab\sqrt{a}-12\sqrt{a}=-5\sqrt{a}\)
Đúng 1
Bình luận (0)
Rút gọn các biểu thức sau:
\(A=\dfrac{a^2-1}{3}\sqrt{\dfrac{9}{\left(1-a\right)^2}}\) với a < 1
\(B=\sqrt{\left(3a-5\right)^2}-2a+4\) với a < \(\dfrac{1}{2}\)
\(C=4a-3-\sqrt{\left(2a-1\right)^2}\) với a < 2
\(D=\dfrac{a-2}{4}\sqrt{\dfrac{16a^4}{\left(a-2\right)^2}}\) với a < 2
a) Ta có: \(A=\dfrac{a^2-1}{3}\cdot\sqrt{\dfrac{9}{\left(1-a\right)^2}}\)
\(=\dfrac{\left(a+1\right)\cdot\left(a-1\right)}{3}\cdot\dfrac{3}{\left|1-a\right|}\)
\(=\dfrac{\left(a+1\right)\left(a-1\right)}{1-a}\)
=-a-1
b) Ta có: \(B=\sqrt{\left(3a-5\right)^2}-2a+4\)
\(=\left|3a-5\right|-2a+4\)
\(=5-3a-2a+4\)
=9-5a
c) Ta có: \(C=4a-3-\sqrt{\left(2a-1\right)^2}\)
\(=4a-3-\left|2a-1\right|\)
\(=4a-3-2a+1\)
\(=2a-2\)
d) Ta có: \(D=\dfrac{a-2}{4}\cdot\sqrt{\dfrac{16a^4}{\left(a-2\right)^2}}\)
\(=\dfrac{a-2}{4}\cdot\dfrac{4a^2}{\left|a-2\right|}\)
\(=\dfrac{a^2\left(a-2\right)}{-\left(a-2\right)}\)
\(=-a^2\)
Đúng 2
Bình luận (0)