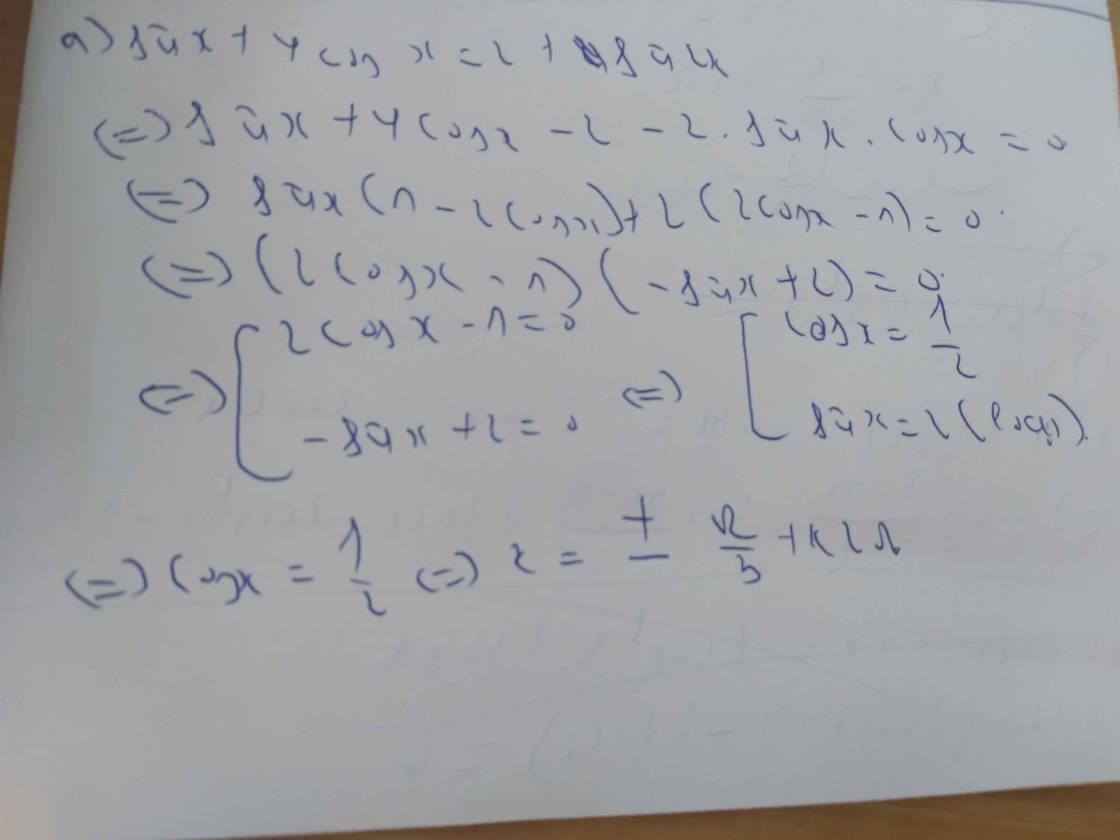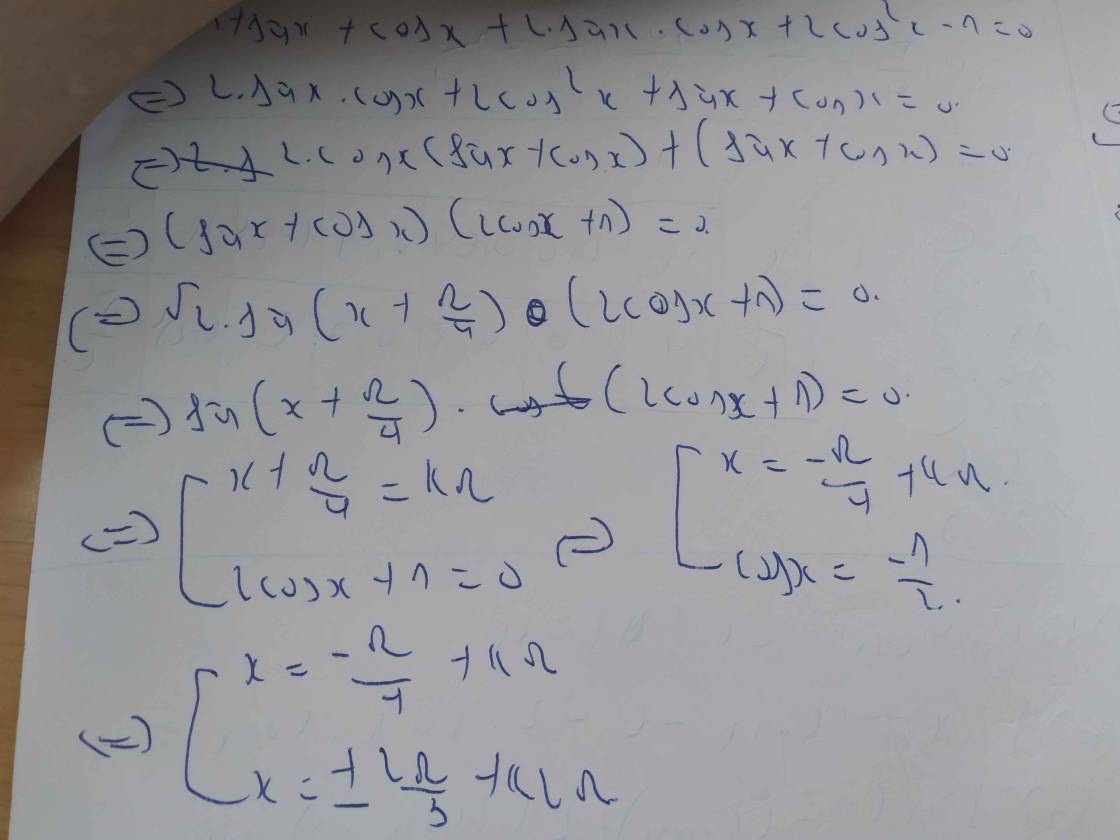\(\lim\limits_{x\rightarrow\infty}\dfrac{1+Sin2x-Cos2x}{1-Sin2x-Cos2x}\)
MA
Những câu hỏi liên quan
Tìm các giới hạn :
a) \(\lim\limits_{x\rightarrow1}\dfrac{x^2-5x+6}{x-2}\)
b) \(\lim\limits_{x\rightarrow\dfrac{\pi}{8}}\dfrac{\sin2x-\cos2x}{8x-\pi}\)
a/ \(\lim\limits_{x\to 1} f(x)=\frac{x^{2}-5x + 6}{x-2} \)
\(<=>\lim\limits_{x\to 1} f(x)=\dfrac{(x-3)(x-2)}{x-2} \)
<=>\(\lim\limits_{x\to 1} f(x)=x-3 \)
\(<=>\lim\limits_{x\to 1} f(x)=-2\)
Đúng 0
Bình luận (0)
tính giới hạn
a) \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{x^2+x+1}\)
b) \(\lim\limits_{x\rightarrow+\infty}\dfrac{3x+1}{3x^2-x+5}\)
c) \(\lim\limits_{x\rightarrow-\infty}\dfrac{3x+5}{\sqrt{x^2+x}}\)
d) \(\lim\limits_{x\rightarrow+\infty}\dfrac{-5x+1}{\sqrt{3x^2+1}}\)
`a)lim_{x->+oo}[x+1]/[x^2+x+1]`
`=lim_{x->+oo}[1/x+1/[x^2]]/[1+1/x+1/[x^2]]`
`=0`
`b)lim_{x->+oo}[3x+1]/[3x^2-x+5]`
`=lim_{x->+oo}[3/x+1/[x^2]]/[3-1/x+5/[x^2]]`
`=0`
`c)lim_{x->-oo}[3x+5]/[\sqrt{x^2+x}]`
`=lim_{x->-oo}[3+5/x]/[-\sqrt{1+1/x}]`
`=-3`
`d)lim_{x->+oo}[-5x+1]/[\sqrt{3x^2+1}]`
`=lim_{x->+oo}[-5+1/x]/[\sqrt{3+1/[x^2]}]`
`=-5/3`
Đúng 2
Bình luận (0)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{4x^2-2}+\sqrt[3]{x^3+1}}{\sqrt{x^2+1}-x}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2x+3}{\sqrt{2x^2-3}}\)
\(\lim\limits_{x\rightarrow\pm\infty}\dfrac{2x^2-1}{3-x^2}\)
a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{\dfrac{4x^2}{x^2}-\dfrac{2}{x^2}}-x\sqrt[3]{\dfrac{x^3}{x^3}+\dfrac{1}{x^3}}}{-x\sqrt{\dfrac{x^2}{x^2}+\dfrac{1}{x^2}}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{4}-1}{-1-1}=\dfrac{3}{2}\)
b/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{2x}{x}+\dfrac{3}{x}}{-\sqrt{\dfrac{2x^2}{x^2}-\dfrac{3}{x^2}}}=\dfrac{2}{-\sqrt{2}}=-\sqrt{2}\)
c/ \(\lim\limits_{x\rightarrow\pm\infty}\dfrac{\dfrac{2x^2}{x^2}-\dfrac{1}{x^2}}{\dfrac{3}{x^2}-\dfrac{x^2}{x^2}}=\dfrac{2}{-1}=-2\)
Đúng 1
Bình luận (0)
tính giới hạn
a) \(\lim\limits_{x\rightarrow+\infty}\dfrac{5x^2+x^3+5}{4x^3+1}\)
b) \(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2-x+1}{x^3+x-2x^2}\)
c) \(\lim\limits_{x\rightarrow-\infty}\dfrac{2x^2-x+1}{x^3+x-2x^2}\)
`a)lim_{x->+oo}[5x^2+x^3+5]/[4x^3+1]` `ĐK: 4x^3+1 ne 0`
`=lim_{x->+oo}[5/x+1+5/[x^3]]/[4+1/[x^3]]`
`=1/4`
`b)lim_{x->-oo}[2x^2-x+1]/[x^3+x-2x^2]` `ĐK: x ne 0;x ne 1`
`=lim_{x->-oo}[2/x-1/[x^2]+1/[x^3]]/[1+1/[x^2]-2/x]`
`=0`
Câu `c` giống `b`.
Đúng 2
Bình luận (0)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2x-\sqrt{3x^2+2}}{5x+\sqrt{x^2+1}}\)
\(\lim\limits_{x\rightarrow+\infty}\sqrt{\dfrac{x^2+1}{2x^4+x^2-3}}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{1+x^4+x^6}}{\sqrt{1+x^3+x^4}}\)
1/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{2x}{x}-\sqrt{\dfrac{3x^2}{x^2}+\dfrac{2}{x^2}}}{\dfrac{5x}{x}+\sqrt{\dfrac{x^2}{x^2}+\dfrac{1}{x^2}}}=\dfrac{2-\sqrt{3}}{5+1}=\dfrac{2-\sqrt{3}}{6}\)
2/ \(=\lim\limits_{x\rightarrow+\infty}\sqrt{\dfrac{\dfrac{x^2}{x^4}+\dfrac{1}{x^4}}{\dfrac{2x^4}{x^4}+\dfrac{x^2}{x^4}-\dfrac{3}{x^4}}}=0\)
3/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt[3]{\dfrac{x^6}{x^6}+\dfrac{x^4}{x^6}+\dfrac{1}{x^6}}}{\sqrt{\dfrac{x^4}{x^4}+\dfrac{x^3}{x^4}+\dfrac{1}{x^4}}}=-1\)
Đúng 1
Bình luận (0)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{3x^3+1}-\sqrt{2x^2+x+1}}{\sqrt[4]{4x^4+2}}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2x+1\right)^3\left(x+2\right)^4}{\left(3-2x\right)^7}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{4x^2-3x+4}-2x}{\sqrt{x^2+x+1}-x}\)
Da nan roi mang meo lam mat het bai -.-
1/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt[3]{\dfrac{3x^3}{x^3}+\dfrac{1}{x^3}}+\sqrt{\dfrac{2x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}{-\sqrt[4]{\dfrac{4x^4}{x^4}+\dfrac{2}{x^4}}}=\dfrac{-\sqrt[3]{3}-\sqrt{2}}{\sqrt[4]{4}}\)
2/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{8x^7}{\left(-2x^7\right)}=-\dfrac{8}{2^7}\)
3/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(4x^2-3x+4-4x^2\right)\left(\sqrt{x^2+x+1}+x\right)}{\left(x^2+x+1-x^2\right)\left(\sqrt{4x^2-3x+4}+2x\right)}=\dfrac{-3.2}{2}=-3\)
Đúng 1
Bình luận (0)
Tìm các giới hạn sau:limlimits_{xrightarrow-infty} dfrac{sqrt{x^6+2}}{3text{x}^3-1}limlimits_{xrightarrow+infty} dfrac{sqrt{x^6+2}}{3text{x}^3-1}limlimits_{xrightarrow-infty} left(sqrt{2text{x}^2+1}+xright)limlimits_{xrightarrow1} dfrac{2text{x}^3-5text{x}-4}{left(x+1right)^2}
Đọc tiếp
Tìm các giới hạn sau:
\(\lim\limits_{x\rightarrow-\infty}\) \(\dfrac{\sqrt{x^6+2}}{3\text{x}^3-1}\)
\(\lim\limits_{x\rightarrow+\infty}\) \(\dfrac{\sqrt{x^6+2}}{3\text{x}^3-1}\)
\(\lim\limits_{x\rightarrow-\infty}\) \(\left(\sqrt{2\text{x}^2+1}+x\right)\)
\(\lim\limits_{x\rightarrow1}\) \(\dfrac{2\text{x}^3-5\text{x}-4}{\left(x+1\right)^2}\)
Tính giới hạn
a) \(\lim\limits_{x\rightarrow-\infty}\dfrac{x+3}{3x-1}=\dfrac{1}{3}\)
b) \(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2-2x+4}-x}{3x-1}\)
a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{x}{x}+\dfrac{3}{x}}{\dfrac{3x}{x}-\dfrac{1}{x}}=\dfrac{1}{3}\)
b/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{\dfrac{x^2}{x^2}-\dfrac{2x}{x^2}+\dfrac{4}{x^2}}-\dfrac{x}{x}}{\dfrac{3x}{x}-\dfrac{1}{x}}=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
\(sinx+4cosx=2+sin2x\)
\(\left(1-sin2x\right)\left(sinx+cosx\right)=cos2x\)
\(1+sinx+cosx+sin2x+cos2x=0\)
\(sinx+sin2x+sin3x=1+cosx+cos2x\)
\(sin^22x-cos^28x=sin\left(\dfrac{17\pi}{2}+10x\right)\)