Làm giúp mình câu 4 với cảm ơn ạ
PH
Những câu hỏi liên quan
Giúp mình làm câu 4 với ạ !!!! Cảm ơn mọi người nhiều !!
Gọi số lượng công việc của đội 1 và 2 làm được trong 1h lần lượt là a,b(phần công việc) \(\left(a,b>0\right)\),x là công việc cần làm \(\left(x>0\right)\)
Theo đề,ta có: \(\left\{{}\begin{matrix}\dfrac{18}{5}\left(a+b\right)=x\left(1\right)\\\dfrac{x}{b}-\dfrac{x}{a}=3\left(2\right)\end{matrix}\right.\)
Từ (2) \(\Rightarrow x\left(\dfrac{1}{b}-\dfrac{1}{a}\right)=3\Rightarrow x=\dfrac{3}{\dfrac{1}{b}-\dfrac{1}{a}}=\dfrac{3}{\dfrac{a-b}{ab}}=\dfrac{3ab}{a-b}\)
Thế vào (1),ta được: \(\dfrac{18}{5}\left(a+b\right)=\dfrac{3ab}{a-b}\Leftrightarrow\dfrac{18\left(a+b\right)}{5}=\dfrac{3ab}{a-b}\)
\(\Rightarrow18\left(a+b\right)\left(a-b\right)=15ab\Rightarrow18a^2-15ab-18b^2=0\)
\(\Rightarrow6a^2-5ab-6b^2=0\Rightarrow\left(3a+2b\right)\left(2a-3b\right)=0\)
mà \(a,b>0\Rightarrow2a=3b\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}b\\b=\dfrac{2}{3}a\end{matrix}\right.\)
Thế vào (1),ta được: \(\left\{{}\begin{matrix}\dfrac{18}{5}\left(a+\dfrac{2}{3}a\right)=x\\\dfrac{18}{5}\left(\dfrac{3}{2}b+b\right)=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a=x\\9b=x\end{matrix}\right.\)
\(\Rightarrow\) đội 1 làm xong công việc trong 6h,đội 2 làm xong trong 9h
Đúng 1
Bình luận (0)
ai giúp mình với minh cảm ơn nhìu ạ. làm câu nào nào cũng được ạ mình cảm ơn 
Ai làm giúp mình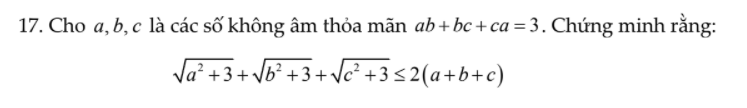 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.
\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)
Đúng 0
Bình luận (0)
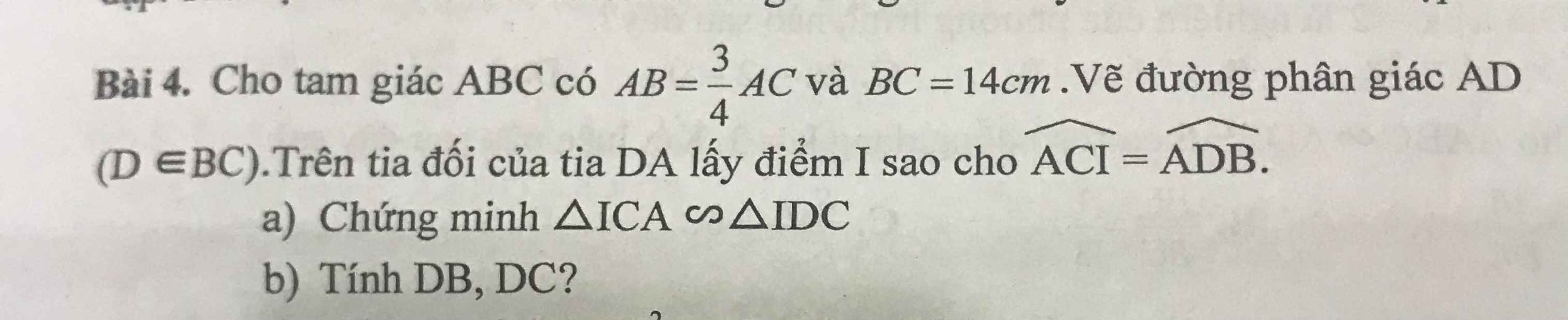
Làm giúp mình câu b với ạ. Mình xin cảm ơn
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
Đúng 0
Bình luận (0)
Ai làm giúp mình 2 câu này với ạ! Mình cảm ơn.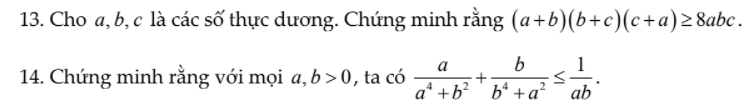
1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)
Đúng 1
Bình luận (0)
Làm giúp mình câu 3 hình với ạ, mình cảm ơn :3
Bạn tham khảo:
Làm hộ mình câu 3 hình với ạ ^^ - Hoc24
Đúng 0
Bình luận (1)
Mọi người ơi giúp mình làm câu 2 và câu 3 với ạ!! Mình xin cảm ơn rất nhiều ạ!
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình làm 2 câu này với ạ! Mình đang cần gấp! Mình xin cảm ơn trước ạ.







