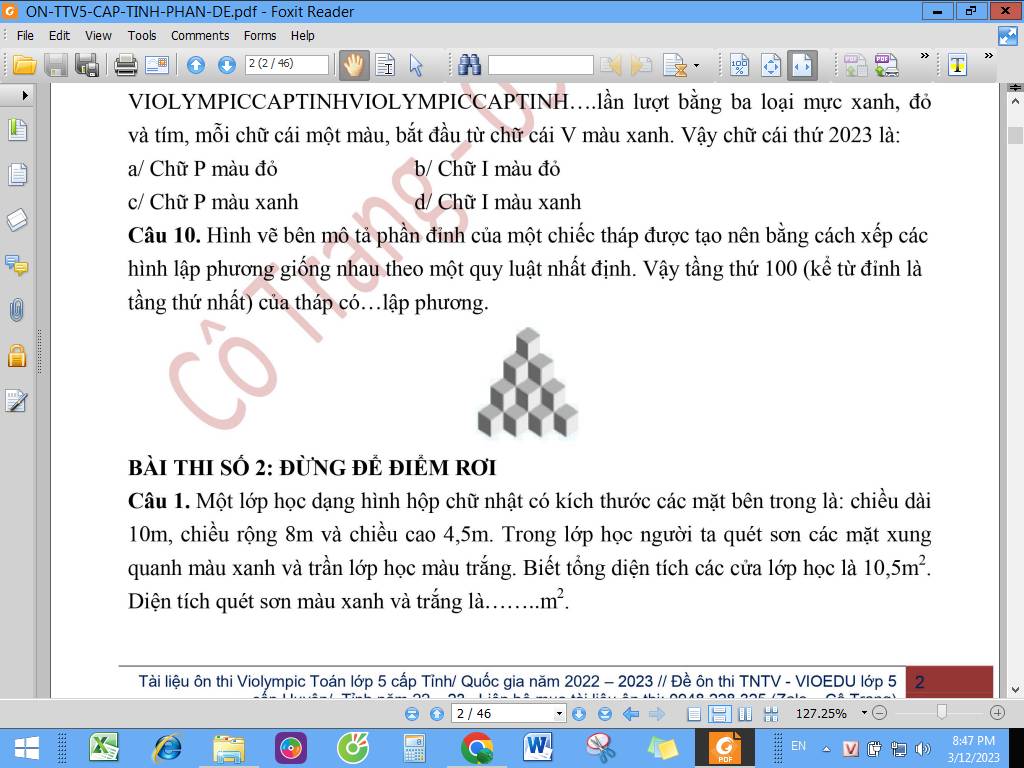
giảng hộ em câu 10 với ạ
H24
Những câu hỏi liên quan
giảng hộ em câu 5 với ạ

5.1
Do \(a\ge c\Rightarrow\left(a+1\right)^2\ge\left(c+1\right)^2\Rightarrow\dfrac{1}{\left(c+1\right)^2}\ge\dfrac{1}{\left(a+1\right)^2}\)
\(P=\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{2}{\left(b+1\right)^2}+\dfrac{2}{\left(c+1\right)^2}\ge\dfrac{2}{\left(a+1\right)^2}+\dfrac{2}{\left(b+1\right)^2}+\dfrac{2}{\left(c+1\right)^2}\)
Áp dụng BĐT Bunhiacopxki:
\(\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}=\dfrac{1}{\left(\sqrt{ab}.\sqrt{\dfrac{a}{b}}+1.1\right)^2}+\dfrac{1}{\left(\sqrt{ab}.\sqrt{\dfrac{b}{a}}+1.1\right)^2}\ge\dfrac{1}{\left(ab+1\right)\left(\dfrac{a}{b}+1\right)}+\dfrac{1}{\left(ab+1\right)\left(\dfrac{b}{a}+1\right)}=\dfrac{1}{ab+1}\)
Tương tự:
\(\dfrac{1}{\left(b+1\right)^2}+\dfrac{1}{\left(c+1\right)^2}\ge\dfrac{1}{bc+1}\)
\(\dfrac{1}{\left(c+1\right)^2}+\dfrac{1}{\left(a+1\right)^2}\ge\dfrac{1}{ca+1}\)
Cộng vế:
\(P\ge\dfrac{1}{ab+1}+\dfrac{1}{bc+1}+\dfrac{1}{ca+1}\ge\dfrac{9}{ab+bc+ca+3}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(a=b=c=1\)
Đúng 0
Bình luận (0)
5.2
Ta có:
\(\dfrac{1}{2a+3b+3c}=\dfrac{1}{\left(a+b\right)+\left(b+c\right)+\left(b+c\right)+\left(c+a\right)}\le\dfrac{1}{16}\left(\dfrac{1}{a+b}+\dfrac{2}{b+c}+\dfrac{1}{c+a}\right)\)
Tương tự:
\(\dfrac{1}{3a+2b+3c}\le\dfrac{1}{16}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{2}{c+a}\right)\)
\(\dfrac{1}{3a+3b+2c}\le\dfrac{1}{16}\left(\dfrac{2}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\)
Cộng vế:
\(P\le\dfrac{1}{16}\left(\dfrac{4}{a+b}+\dfrac{4}{b+c}+\dfrac{4}{c+a}\right)=505\)
\(P_{max}=505\) khi \(a=b=c=\dfrac{3}{4040}\)
Đúng 0
Bình luận (0)
giảng hộ em câu 3.2 với ạ
3.2
\(\Delta'=\left(a+1\right)^2-2a=a^2+1>0;\forall a\Rightarrow\) pt luôn có 2 nghiệm pb với mọi a
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(a+1\right)\\x_1x_2=2a\end{matrix}\right.\)
Do \(x_1\) là nghiệm nên: \(x_1^2-2\left(a+1\right)x_1+2a=0\Rightarrow x_1^2=2\left(a+1\right)x_1-2a\)
Thay vào bài toán:
\(2\left(a+1\right)x_1-2a+x_1-x_2=3-2a\)
\(\Leftrightarrow\left(2a+3\right)x_1-x_2=3\)
\(\Rightarrow x_2=\left(2a+3\right)x_1-3\)
Thế vào \(x_1+x_2=2\left(a+1\right)\)
\(\Rightarrow x_1+\left(2a+3\right)x_1-3=2\left(a+1\right)\)
\(\Rightarrow\left(2a+4\right)x_1=2a+5\Rightarrow x_1=\dfrac{2a+5}{2a+4}\Rightarrow x_2=2a+2-\dfrac{2a+5}{2a+4}=\dfrac{4a^2+10a+3}{2a+4}\) (\(a\ne-2\))
Thế vào \(x_1x_2=2a\)
\(\Rightarrow\dfrac{\left(2a+5\right)\left(4a^2+10a+3\right)}{\left(2a+4\right)^2}=2a\)
\(\Rightarrow8a^2+24a+15=0\Rightarrow a=...\)
Đúng 1
Bình luận (0)
mọi người giảng hộ em câu này với ạ , em cảm ơn mọi người trước
Tìm x :
4x(x-5) - (x-1) . (4x - 3) = 5
\(\Leftrightarrow4x^2-20x-4x^2+3x+12x-3=5\)
\(\Leftrightarrow-5x=8\)
hay \(x=-\dfrac{8}{5}\)
Đúng 0
Bình luận (0)
có ai làm hộ em câu 10 và 11 này với đc ko em cảm ơn ạ!

Câu 1 :
\(\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\) ?
Các anh chị chỉ cho em cách tính với ạ !! Trình bày cụ thể hộ em với
\(\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\dfrac{2^{30}+2^{20}}{2^{12}+2^{22}}=\dfrac{2^{20}\left(2^{10}+1\right)}{2^{12}\left(2^{10}+1\right)}=2^8=256\)
Đúng 0
Bình luận (0)
chỉ cách tính hay là có cần tính kết quả luôn k bn
Đúng 0
Bình luận (0)
anh chị nào giảng hộ em bài hai góc đối đỉnh đi ạ!
TL :
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia .
Hok tốt
Đúng 0
Bình luận (0)
TRẢ LỜI:Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Bạn có thể tham khảo trong SGK nhé!
Có bài nào ko hiểu về hai góc đối đỉnh thì cứ lên online math tìm sự trợ giúp nha
#học tốt#
Đúng 0
Bình luận (0)
1. Định nghĩa : Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia
2. Tính chất : Hai góc đối đỉnh thì bằng nhau
Đúng 0
Bình luận (0)
Giúp em làm câu 4 tự luận được không ạ, nếu có thể thì ib em, giảng lại cho em với. Em cảm ơn ạaa
chứng tỏ rằng 2n+3 và 7n+10 là hai số nguyên tố cùng nhau .
câu trả lời nó nghi thế nhưng em ko nghĩ đc ra
mong anh chi giảng hộ chi tiết hơn
Gọi d=ƯCLN(2n+3;7n+10)
=>2n+3 chia hết cho d và 7n+10 chia hết cho d
=>14n+21 chia hết cho d và 14n+20 chia hết cho d
=>1 chia hết cho d
=>d=1
=>2n+3 và 7n+10 là hai số nguyên tố cùng nhau
Đúng 3
Bình luận (0)
Gọi (2n+3,7n+10)=d
=>2n+3⋮d =>14n+21⋮d
7n+10⋮d => 14n+20⋮d
=>(14n+21)-(14n+20)⋮d
=>1⋮d =>d=1
Vậy 2n+3 và 7n+10 là 2 số nguyên tố cùng nhau
Đúng 3
Bình luận (0)
Làm hộ em Câu 10 trc 9h30p tối nay,em tick cho ạ![]()