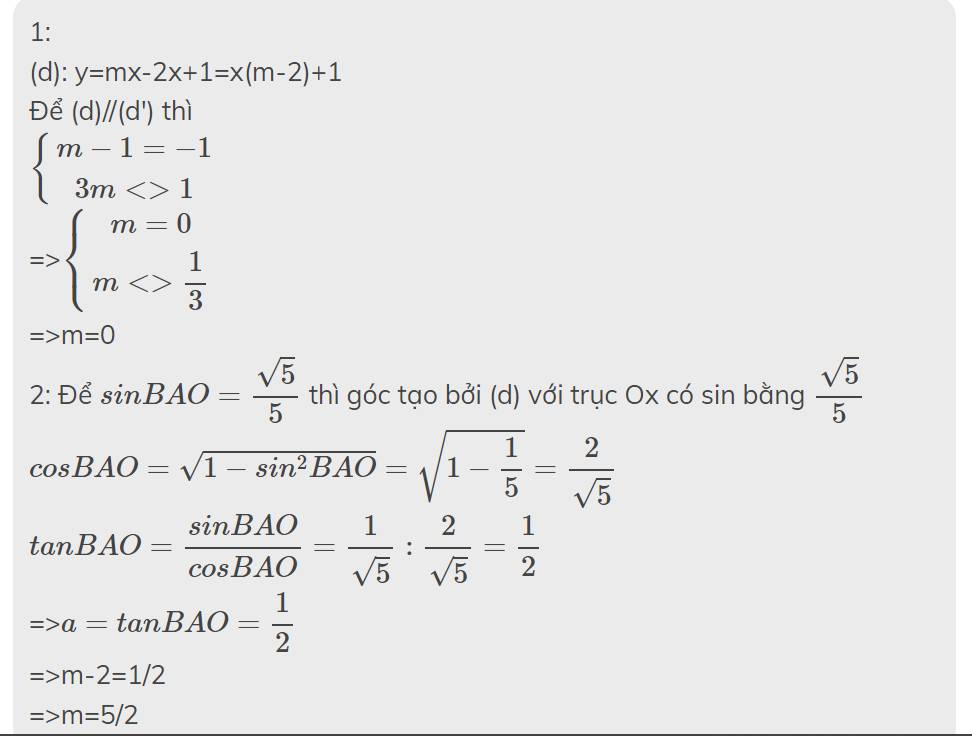Cho m\(\ge\)-3.Tìm GTLN của A=-3m2+2m+32
TD
Những câu hỏi liên quan
Cho m\(\ge\)-3.Tìm GTLN của A=-3m2+2m+32
Cho m\(\ge\)-3.Tìm GTLN của A=-3m2+2m+32
Bài này cũng tương tự với câu trước đó thôi nhé Trương Tuấn Dũng ^^
Ta có : \(A=-3m^2+2m+32=-3\left(m-\frac{1}{3}\right)^2+\frac{97}{3}\)
\(m\ge-3\Leftrightarrow-3\left(m-\frac{1}{3}\right)^2\le-\frac{100}{3}\Rightarrow A\le-1\)
Vậy Max A = -1 <=> m = -3
Đúng 0
Bình luận (0)
À , kết quả của mình sai rồi nhé ^^
Đúng 0
Bình luận (0)
Tìm GTLN của A = (2m^2-4m+5)/(m^2-2m+2)
\(A=\frac{2m^2-4m+5}{m^2-2m+2}=\frac{3\left(m^2-2m+2\right)-\left(m^2-2m+1\right)}{m^2-2m+2}\)
\(=3-\frac{\left(m-1\right)^2}{m^2-2m+2}\le3do\hept{\begin{cases}\left(m-1\right)^2\ge0\\\left(m-1\right)^2+1>0\end{cases}\Rightarrow\frac{\left(m-1\right)^2}{m^2-2+2}\ge0}\)
dấu ''='' xay ra khi và chỉ khi x=1
VẬY GTLN CỦA ALAF 3 TẠI X=1
Đúng 0
Bình luận (0)
cho pt x^2 + m^2 -2m+5-x-3 =0 . tìm GTLN của tổng 2 nghiệm của pt
Cho x\(\ge-\dfrac{1}{2}\). Tìm GTLN của A=\(\sqrt{2x^2+5x+2}+2\sqrt{x+3}-2x\)
Áp dụng BĐT cosi:
\(A=\sqrt{\left(2x+1\right)\left(x+2\right)}+2\sqrt{x+3}-2x\\ A\le\dfrac{2x+1+x+2}{2}+\dfrac{4+x+3}{2}-2x\\ A\le\dfrac{3x+3}{2}+\dfrac{x+7}{2}-2x=\dfrac{3x+3+x+7-4x}{2}=5\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}2x+1=x+2\\4=x+3\end{matrix}\right.\Leftrightarrow x=1\)
Đúng 4
Bình luận (0)
cho x=1-2m , y=-3-4m tìm m để x.y đạt GTLN
Bạn kiểm tra lại đề, nếu x và y theo m đúng thế này thì \(xy\) chỉ có GTNN chứ không có GTLN
Đúng 0
Bình luận (0)
Cho m\(\ge\)-3.Tìm GTNN của P=2m2+30m+72
Ta có : \(P=2m^2+30m+72=2\left(m+\frac{15}{2}\right)^2-\frac{81}{2}\)
Vì \(m\ge3\Leftrightarrow2\left(m+\frac{15}{2}\right)^2\ge\frac{441}{2}\Leftrightarrow P\ge180\)
Vậy Min \(P=180\Leftrightarrow m=3\)
Đúng 0
Bình luận (0)
Cho (d):y=mx-2m+1 (m tham số)
1. Tìm m để (d)//(d') biết (d'):y=-x+3m
2. Tìm m để (d) cắt 2 trục Ox, Oy lần lượt ở A, B phân biệt thỏa mãn sinBAO = \(\dfrac{\sqrt{5}}{5}\), với O là gốc tọa
Tìm GTLN của biểu thức:\(A=\frac{2m^2-4m+5}{m^2-2m+2}\)
Ta có: \(A=\frac{2m^2-4m+5}{m^2-2m+2}\)
\(=\frac{2m^2-4m+2+3}{m^2-2m+1+1}=\frac{2\left(m^2-2m+1\right)+3}{\left(m^2-2m+1\right)+1}\)
\(=\frac{2\left(m-1\right)^2+3}{\left(m-1\right)^2+1}\ge\frac{3}{1}=3\) (do \(\left(m-1\right)^2\ge0\))
Dấu "=" xảy ra \(\Leftrightarrow m-1=0\Leftrightarrow m=1\)
Vậy \(A_{min}=3\Leftrightarrow m=1\)
Đúng 0
Bình luận (0)
\(A=2+\frac{1}{m^2-2m+1+1}=2+\frac{1}{\left(m-1\right)^2+1}\)
\(\left(m-1\right)^2+1\ge1\Leftrightarrow\frac{1}{\left(m-1\right)^2+1}\le1\)
\(\Rightarrow A\le3\)
\("="\Leftrightarrow m=1\)