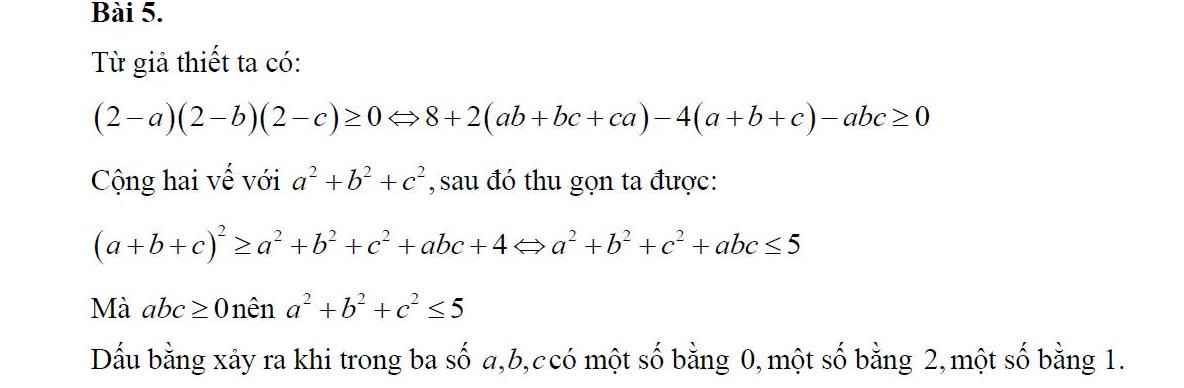cho x,y>0 thỏa mãn\(x^3+y^3=2\) CMR \(x^2+y^2\le2\)
DN
Những câu hỏi liên quan
Cho x >0; y> 0 thỏa mãn \(x^2+y^2\le x+y\)
CMR \(x+3y\le2+\sqrt{5}\)
Cho các số thực dương x,y thỏa mãn x+y=2. CMR: \(x^5y^3+y^5x^3\le2\)
\(VT=x^3y^3\left(x^2+y^2\right)=\frac{1}{8}.2xy.2xy.2xy.\left(x^2+y^2\right)\)
\(\le\frac{1}{8}\left[\frac{\left(4xy+2xy+x^2+y^2\right)^4}{256}\right]\)(áp dụng BĐT AM-GM cho 4 số)
\(=\frac{1}{8}.\frac{\left[4xy+\left(x+y\right)^2\right]^4}{256}\le\frac{1}{8}.\frac{\left[2\left(x+y\right)^2\right]^4}{256}=2\)
Đẳng thức xảy ra khi x = y = 1
Ta có đpcm/
Đúng 0
Bình luận (0)
Cho các số không âm x,y thỏa mãn\(x^3+y^3\) = 2 .CMR : \(x^2+y^2\le2\)
Áp dụng BĐT Bunhiacôpxki , ta có :
\(\left(x^2+y^2\right)^2=\left(\sqrt{x}.\sqrt{x^3}+\sqrt{y}.\sqrt{y^3}\right)^2\) \(\le\left(x+y\right)\left(x^3+y^3\right)=2\left(x+y\right)\)
\(\Leftrightarrow\left(x^2+y^2\right)^4\le4\left(x+y\right)^2=4\left(1.x+1.y\right)^2\le4\left(1+1\right)\left(x^2+y^2\right)=8\left(x^2+y^2\right)\)
\(\Leftrightarrow\left(x^2+y^2\right)^3\le8\)
\(\Leftrightarrow x^2+y^2\le2\left(\text{đ}pcm\right)\)
Dấu "=" xảy ra khi x = y = 1
Đúng 0
Bình luận (0)
B1: Cho 0le a,b,cle2 thỏa mãn a+b+c3. CMR: a^2+b^2+c^2le5B2: Cho a,bge0 thỏa mãn a^2+b^2a+b. TÌm GTLN Sdfrac{a}{a+1}+dfrac{b}{b+1}B3: CMR: dfrac{1}{left(x-yright)^2}+dfrac{1}{x^2}+dfrac{1}{y^2}gedfrac{4}{xy}forall xne y,xyne0
Đọc tiếp
B1: Cho \(0\le a,b,c\le2\) thỏa mãn \(a+b+c=3\). CMR: \(a^2+b^2+c^2\le5\)
B2: Cho \(a,b\ge0\) thỏa mãn \(a^2+b^2=a+b\). TÌm GTLN \(S=\dfrac{a}{a+1}+\dfrac{b}{b+1}\)
B3: CMR: \(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\forall x\ne y,xy\ne0\)
Bài 3:
\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)
\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)
Đúng 4
Bình luận (4)
cho x,y>0 thỏa mãn x^2+y^3>=x^3+y^4. cmr x^3+y^3=<2
bài 1: cho x;y là 2 số thực thỏa mãn x^3+ y^3=2
cmr: 0<x+y<=2
bài 2: cho x,y,z >=0 thỏa mãn x+y+z=1
Tìm GTLN của P=22xy +4yz+ 2015zx
cho x,y,z > 0 thỏa mãn x + y + z = 2. Cmr:
\(\sqrt{xy^3+yz^3+zx^3}+\sqrt{x^3y+y^3z+z^3x}\le2\)
Cho x,y là các số thực thỏa mãn \(0\le x\le y\le1;2xy+y\le2\)
Chứng minh rằng :\(2x^2+y^2\le\frac{3}{2}\)
Cho x,y là các số thực thỏa mãn điều kiện \(0\le x,y,z\le2\) và x + y + z = 3.
CMR: \(x^{^2}+y^{^2}+z^{^2}\le5\)
Lời giải:
Do $x,y,z\in [0;2]\Rightarrow (x-2)(y-2)(z-2)\leq 0$
$\Leftrightarrow xyz-2(xy+yz+xz)+4(x+y+z)-8\leq 0$
$\Leftrightarrow 2(xy+yz+xz)\geq 4(x+y+z)-8+xyz$
Mà $4(x+y+z)-8+xyz=4.3-8+xyz=4+xyz\geq 4$ do $x,y,z\geq 0$
Do đó $2(xy+yz+xz)\geq 4$
Suy ra $x^2+y^2+z^2=(x+y+z)^2-2(xy+yz+xz)=9-2(xy+yz+xz)\leq 9-4=5$
Ta có đpcm. Dấu "=" xảy ra khi $(x,y,z)=(2,1,0)$ và các hoán vị.
Có nhiều cách!
Cách 2:Giả sử \(x\ge y\ge z\Rightarrow3x\ge x+y+z=3\Rightarrow2\ge x\ge1\)
Ta có: \(x^2+y^2+z^2\le x^2+y^2+2yz+z^2=x^2+\left(y+z\right)^2\)
\(=x^2+\left(3-x\right)^2=2x^2-6x+9\)
\(=2\left(x-1\right)\left(x-2\right)+5\le5\)
Đẳng thức xảy ra khi \(\left(x;y;z\right)=\left(2;1;0\right)\) và các hoán vị
Vậy...
Cách 3: Dùng khai triển Abel: Câu hỏi của Thảo Lê - Toán lớp 8 - Học toán với OnlineMath (em không chắc lắm nhưng cứ đăng)