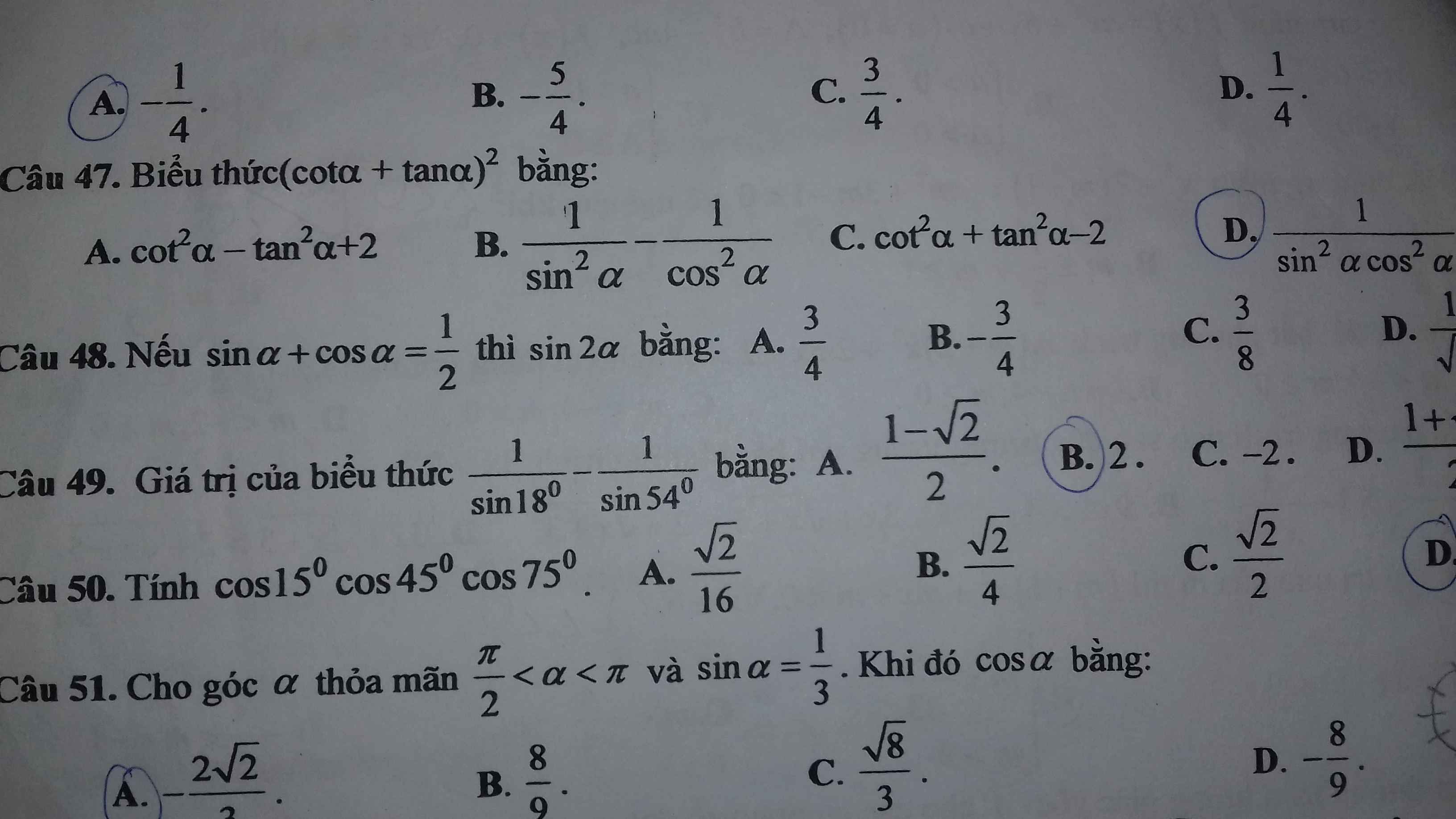
47.

\(\left(cot\alpha+tan\alpha\right)^2=\left(\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{cos\alpha}\right)^2=\left(\dfrac{cos^2\alpha+sin^2\alpha}{sin\alpha.cos\alpha}\right)^2=\dfrac{1}{sin^2\alpha.cos^2\alpha}\)

(cota +tana)\(^2\)=cot\(^2\)a+2cota.tana+tan\(^2\)a=(cot\(^2\)a +1)+(tan\(^2\)+1)=\(\dfrac{1}{sin^2a}\)+\(\dfrac{1}{cos^2a}\)=\(\dfrac{cos^2a+sin^2a}{cos^2a.sin^2a}\)=\(\dfrac{1}{cos^2a.sin^2a}\)

\((\cot\alpha+\tan\alpha)\)² \(=\dfrac{\cos^2\alpha}{\sin^2\alpha}+\dfrac{\sin^2\alpha}{\cos^2\alpha}+2\dfrac{\cos}{\sin}\dfrac{\sin}{\cos}\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha}{\sin^2\alpha.\cos^2\alpha}+2\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha+2\sin^2\alpha.\cos^2\alpha}{\sin^2\alpha.\cos^2\alpha}\)\(=\dfrac{(\cos^2\alpha+\sin^2\alpha)^2}{\sin^2\alpha.\cos^2\alpha}\)
mà : \(\sin^2+\cos^2=1\)
\(\Rightarrow\)\((\cot\alpha+\tan\alpha)\)²\(=\)\(\dfrac{1}{\sin^2\alpha.\cos^2\alpha}\)
\(\Rightarrow\)Đáp án: D

Số tập con của P là \(2^n\Rightarrow C\) là đáp án

 31 - [ 26 - ( 209 + 35 ) ] 

= 31 - ( 26 - 344 )

=31 - ( -318)

= 31 + 318 ( trừ trừ thành cộng nha )

= 349

31-(26-(209+35)=31-

hok tốt

k cho mik

kb nữa nhé

Sao bạn trả lời giữa chừng thía 

\(U=IR=1,2\cdot10=12V\)

Chọn C

:D

D

d

Câu 11: A

Câu 12: C

a: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)

Xét ΔABC có AD là phân giác

nên BD/AB=CD/AC

=>BD/12=CD/16

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{12}=\dfrac{CD}{16}=\dfrac{BD+CD}{12+16}=\dfrac{20}{28}=\dfrac{5}{7}\)

Do đó: BD=60/7(cm); CD=80/7(cm)

b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

B C 2 = A B 2 + A C 2 = 12 2 + 6 2 = 400

Suy ra: BC =20 (cm)

Vì AD là đường phân giác của ∠(BAC) nên:

\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) (tính chất đường phân giác)

Suy ra: 

Suy ra: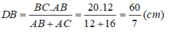 

Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)

Câu 93 

Ta có \(AC^2=AB^2+BC^2-2.AB.BC.cosB=19\Rightarrow AC=\sqrt{19}\)

chọn D