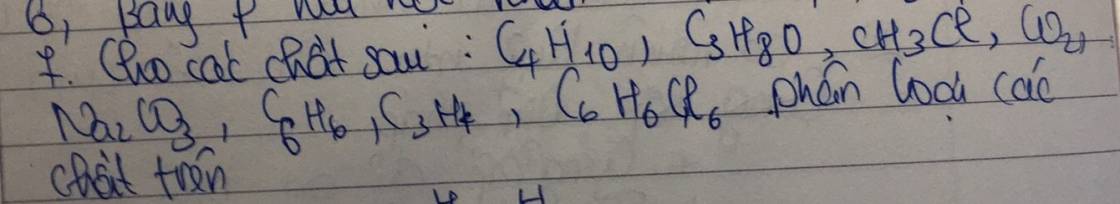
- Hợp chất vô cơ: CO₂, Na₂CO₃ 

- Hợp chất hữu cơ: 

+ Hiđrocacbon: C₄H₁₀, C₆H₆, C₃H₄ 

+ Dẫn xuất của hiđrocacbon: C₃H₈O, CH₃Cl, C₆H₆Cl₆

Câu 1.

Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)

\(;a_i\ne a_j\)

Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.

5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)

\(\Rightarrow\)Có \(A_8^5\) cách.

Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.

c

Câu 7

a,Xét \(\Delta ICA\) và \(\Delta ICB\) ta có :

\(AC=CB\) ( do \(\Delta ABC\) cân tại \(C\) nên 2 cạnh bên bằng nhau )

\(\widehat{CAI} = \widehat{CBI}\) ( hai góc ở đáy )

\(AI=IB \)(do \(I\) là trung điểm của \(AB\))

\(\Rightarrow\Delta ICA=\Delta ICB\left(c.g.c\right)\)

b,Ta có \(CI \) là trung tuyến suất phát từ đỉnh \(C\) 

\(\Rightarrow CI\perp AB\)(tính chất đường trung tuyến trong tam giác cân)

c, Áp dụng định lý \(Pi-ta-go\) vào tam giác vuông \(CIA\) ta có :

\(AC^2=CI^2+IA^2\Rightarrow AC=\sqrt{CI^2+IA^2}\)

\(\Leftrightarrow AC=\sqrt{12^2+5^2}=13\)

\(\Rightarrow AC=BC=13\left(cm\right)\)

Chu vi \(\Delta ABC\) là 

\(AC+CB+AB=13+13+10=36\left(cm\right)\)

Câu 9:

a) Xét ΔAMB và ΔAMC có 

AB=AC(ΔABC cân tại A)

AM chung

MB=MC(M là trung điểm của BC)

Do đó: ΔAMB=ΔAMC(c-c-c)

b) Ta có: ΔAMB=ΔAMC(cmt)

nên \(\widehat{AMB}=\widehat{AMC}\)(hai góc tương ứng)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

hay AM⊥BC(đpcm)

c) Xét ΔKBM vuông tại K và ΔHCM vuông tại H có 

BM=CM(M là trung điểm của BC)

\(\widehat{KBM}=\widehat{HCM}\)(hai góc ở đáy của ΔABC cân tại A)

Do đó: ΔKBM=ΔHCM(cạnh huyền-góc nhọn)

Suy ra: MK=MH(hai cạnh tương ứng)

d) Xét ΔAKM vuông tại K và ΔAHM vuông tại H có 

AM chung

MK=MH(cmt)

Do đó: ΔAKM=ΔAHM(cạnh huyền-cạnh góc vuông)

Suy ra: AK=AH(hai cạnh tương ứng)

Xét ΔAKH có AK=AH(cmt)

nên ΔAKH cân tại A(Định nghĩa tam giác cân)

⇒\(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)

Ta có: ΔABC cân tại A(gt)

nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)

Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)

mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị

nên KH//BC(Dấu hiệu nhận biết hai đường thẳng song song)

Mai mình thi rồi các bạn giúp mình đi mà😭😭