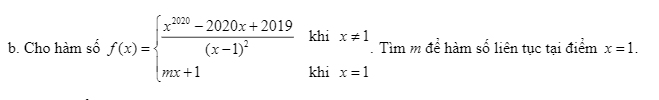
giúp em với em cảm ơn nhiềuuuu
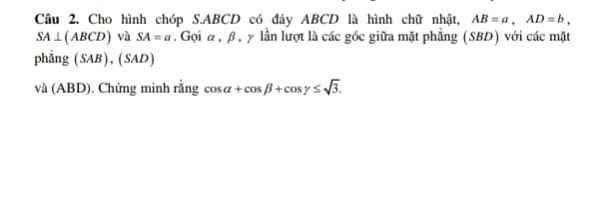
giúp em với em cảm ơn nhiềuuuu
Kẻ \(AE\perp BD\) , \(AF\perp SE\Rightarrow AF\perp\left(SBD\right)\)
Dễ dàng chứng minh \(AD\perp\left(SAB\right)\) ; \(AB\perp\left(SAD\right)\)
Từ đó ta có: \(\alpha=\widehat{FAD}\) ; \(\beta=\widehat{FAB}\) ; \(\gamma=\widehat{FAS}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{2}{a^2}+\dfrac{1}{b^2}=\dfrac{a^2+2b^2}{a^2b^2}\)
\(\Rightarrow AF=\dfrac{ab}{\sqrt{a^2+2b^2}}\)
\(\Rightarrow T=cos\alpha+cos\beta+cos\gamma=\dfrac{AF}{AD}+\dfrac{AF}{AB}+\dfrac{AF}{AS}=\dfrac{ab}{\sqrt{a^2+2b^2}}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow T=\dfrac{\sqrt{3}ab}{\sqrt{\left(1+2\right)\left(a^2+2b^2\right)}}\left(\dfrac{a+2b}{ab}\right)\le\dfrac{\sqrt{3}ab}{a+2b}\left(\dfrac{a+2b}{ab}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)

giúp em với ạ em cảm ơn nhiềuuuu
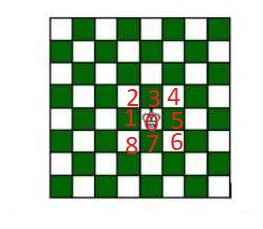
Xung quanh ô quân vua đang đứng có 8 ô, nên ở mỗi một bước, quân vua có 8 cách di chuyển
\(\Rightarrow\) Quân vua có \(8^3\) cách di chuyển 3 bước
Ở bước đầu tiên, quân vua có 3 kiểu đi: sang các ô xanh hoặc sang các ô đỏ
TH1: quân vua sang ô xanh: có 4 cách. Do vai trò các ô như nhau, giả sử quân vua sang ô số 1
Để sau 2 bước nữa quay về ô 0 ban đầu, ở bước tiếp theo nó phải đi vào 1 ô nằm kế ô 0 \(\Rightarrow\) có 4 cách (là các ô 2,3,7,8)
Vậy có 4.4=16 cách
TH2: Quân vua sang ô trắng (có 4 cách) giả sử là ô số 2, vẫn như trên, bước thứ 2 nó phải sang 1 ô nằm kế ô số 0 => có 2 cách
\(\Rightarrow\) 4.2 =8 cách
Vậy quân vua có \(16+8=24\) cách đi thỏa mãn
Xác suất: \(\dfrac{24}{8^3}=...\)
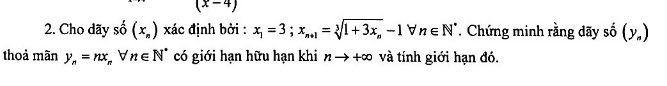
giúp em câu này với ạ em cảm ơn nhiềuuuu
Cho em hỏi đây có phải là 1 lưới thức ăn gồm 3 chuỗi thức ăn trong đó có những mắc xích chung không ạ? Có gì sai sửa giúp em vsss! Em cảm ơn mọi người nhiềuuuu! 
vậy thì lưới thức ăn của bn đúng rồi đấy
Giúp mình với ạ:') Mik cảm ơn nhiềuuuu
xin giúp e với ạ e cảm ơn rất nhiềuuuu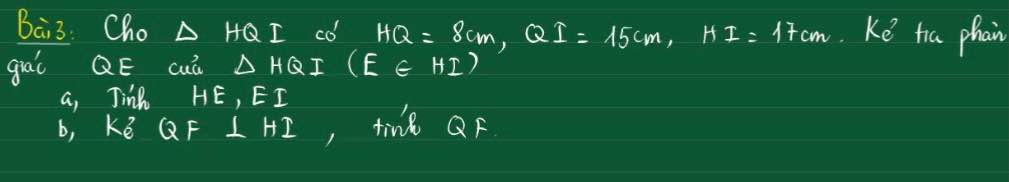

giúp mik gấp với ạ mik cảm ơn rất nhiềuuuu
giải giúp mình bài 5 và bài 6 với
mình cảm ơn rất nhiềuuuu 😖😖
Bài 6:
a: \(Q=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
Mn ơi giải giúp mik bài 3 vs, cảm ơn mn nhiềuuuu nha 😷😊
a: =3/2-2/3:(4/18+3/18)
=3/2-2/3:7/18
=3/2-2/3*18/7
=3/2-12/7
=-3/14
b: =(5/8-1/5)*2-1/4
=5/4-2/5-1/4
=1-2/5=3/5
c: =(3+5/6-1/2):55/12
=10/3*12/55
=8/11