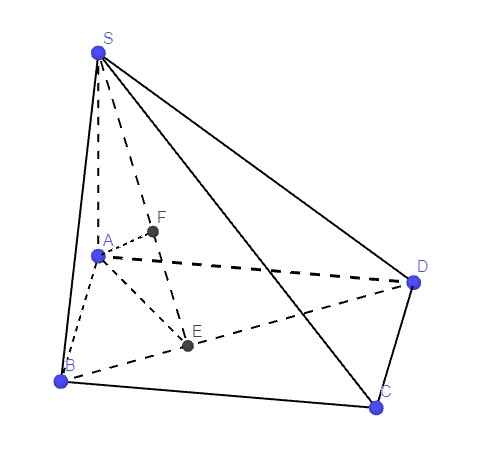
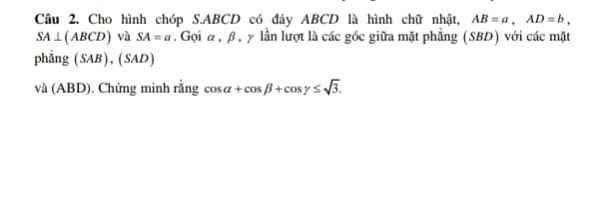Kẻ \(AE\perp BD\) , \(AF\perp SE\Rightarrow AF\perp\left(SBD\right)\)
Dễ dàng chứng minh \(AD\perp\left(SAB\right)\) ; \(AB\perp\left(SAD\right)\)
Từ đó ta có: \(\alpha=\widehat{FAD}\) ; \(\beta=\widehat{FAB}\) ; \(\gamma=\widehat{FAS}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{2}{a^2}+\dfrac{1}{b^2}=\dfrac{a^2+2b^2}{a^2b^2}\)
\(\Rightarrow AF=\dfrac{ab}{\sqrt{a^2+2b^2}}\)
\(\Rightarrow T=cos\alpha+cos\beta+cos\gamma=\dfrac{AF}{AD}+\dfrac{AF}{AB}+\dfrac{AF}{AS}=\dfrac{ab}{\sqrt{a^2+2b^2}}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow T=\dfrac{\sqrt{3}ab}{\sqrt{\left(1+2\right)\left(a^2+2b^2\right)}}\left(\dfrac{a+2b}{ab}\right)\le\dfrac{\sqrt{3}ab}{a+2b}\left(\dfrac{a+2b}{ab}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)