Hai phân số a phần b và c phần d gọi là..........................nếu a.d=b.c
ON
Những câu hỏi liên quan
Chứng tỏ rằng nếu a phần b bằng c phần d thì a.d=b.c và ngược lại
*) Ta có\(\frac{a}{b}=\frac{c}{d}\)
=> \(\frac{a}{b}.bd=\frac{c}{d}.bd\)
=> \(\frac{a.b.d}{b}=\frac{b.c.d}{d}\)
=> a.d = b.c
*) Ta có a.d = b.c
=> \(\frac{a.d}{bd}=\frac{b.c}{bd}\)
=> \(\frac{a}{b}=\frac{c}{d}\)
cho hai số hữu tỉ a/b vsf c/d ( b>0,d>0) . CMR
a) Nếu a/b<c/d thì a.d <b.c b) Nếu a.d<b.c thì a/b < c/d
2. Hai phân số nếu:A. a.c b.d B a.b c.d C. a: c b: d D. a.d b.c
Đọc tiếp
2. Hai phân số ![]() =
=![]() nếu:
nếu:
A. a.c = b.d B a.b = c.d C. a: c = b: d D. a.d = b.c
Xem thêm câu trả lời
Cho 2 số Hữu Tỉ a/b và c/d
Xem chi tiết
(b và d >0)
Chứng minh rằng:
Nếu a/b < c/d thì a.d < b.cNếu a.d < b.c thì a/b < c/dBài toán này rất hay và logic ai giải đc là rất giỏi!!
1.
Nếu \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{ad}{bd}< \frac{cb}{db}\)
\(\Leftrightarrow ad< cd\left(dpcm\right)\)
2
Nếu \(ad< bc\Leftrightarrow\frac{ad}{bd}< \frac{bc}{bd}\)
\(\Leftrightarrow\frac{a}{b}< \frac{c}{d}\left(dpcm\right)\)
Đúng 0
Bình luận (0)
a) cho m,n là hai số nguyên (n>0).So sánh m/n và m+1/n+1
b) cho số hữu tỉ a/b và c/d (b,d>0)
Chứng minh:a/b>c/d nếu a.d>b.c và a.d>b.c nếu a/b>c/d
b)
Để \(\frac{a}{b}>\frac{a+c}{b+d}\) thì \(a.\left(b+d\right)>b.\left(a+c\right)\)
\(\Rightarrow ab+ad>ab+bc\)
\(\Rightarrow ad>bc\)
\(\Rightarrow\frac{a}{b}>\frac{c}{d}\left(đpcm\right).\)
Để \(\frac{a+c}{b+d}>\frac{c}{d}\) thì \(\left(a+c\right).d>\left(b+d\right).c\)
\(\Rightarrow ad+cd>bc+dc\)
\(\Rightarrow ad>bc\)
\(\Rightarrow\frac{a}{b}>\frac{c}{d}\left(đpcm\right).\)
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
Cho 2 số hữu tỉ x=\(\frac{a}{b}\) và y=\(\frac{c}{d}\) trong đó b và d là số nguyên dương, chứng tỏ:
a)Nếu a.d=b.c thì x=y
b)Nếu a.d>b.c thì x>y
c)Nếu x>y thì a.d>b.c
Giải giúp mình câu này nhé. Thanks nhiều
cho 2 số hữu tỉ
a/b và c/d(biết b>0;d>0)
chứng minh rằng a/b < c/d nếu a.d < b.c
chứng minh rằng a.d < b.c nếu a/b < c/d
thanks nhiều
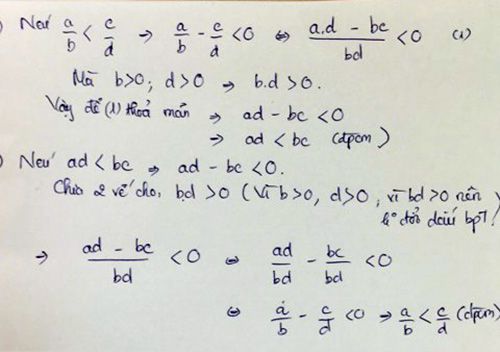
Làm nhắn gọn hơn thì
1
a/b < c/d
=> ad/bd < cb/db
=> ad < cb
2
ad < cb
=>ad /bd < cb/bd
Chúc pn hc tốt
Đúng 0
Bình luận (0)
Cho 2 số hữu tỉ x=\(\frac{a}{b}\) và y=đó b và d là số nguyên dương, chứng tỏ
a)Nếu a.d=b.c thì x=y
b)Nếu a.d>b.c thì x>y
c)Nếu x>y thì a.d>b.c
Cho hai số hữu tỉ a/b; c/d (b>0; d>0). Chứng minh rằng a/b<c/d nếu a.d < b.c ?
Ta có:a/b<c/d =>ad<bc (1)
Thêm ab vào (1) ta đc:
ad+ab<bc+ab hay a(b+d)<b(a+c) =>a/b<a+c/b+d (2)
Thêm cd vào 2 vế của (1), ta lại có:
ad+cd<bc+cd hay d(a+c)<c(b+d) => c/d>a+c/b+d (3)
Từ (2) và (3) suy ra:a/b<a+c/b+d<c/d
Đúng 0
Bình luận (0)



