Chứng minh phương trình \(sin^3x+sinx-1=0\) có ít nhất 1 nghiệm.
LA
Những câu hỏi liên quan
cho phương trình \(2cos2x+sin^2xcosx+sinxcos^2x=m\left(sinx+cosx\right)\)tìm m để phương trình có ít nhất 1 nghiệm thuộc đoạn\(\left[0;\dfrac{\Pi}{2}\right]\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left(2cosx-2sinx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx+cosx\right)=m\left(sinx+cosx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx+cosx=0\left(\text{vô nghiệm trên đoạn xét}\right)\\2cosx-2sinx+sinx.cosx=m\left(1\right)\end{matrix}\right.\)
Xét (1), đặt \(t=cosx-sinx=\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}t\in\left[-1;1\right]\\sinx.cosx=\dfrac{1-t^2}{2}\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2t+\dfrac{1-t^2}{2}=m\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+2t+\dfrac{1}{2}\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=2\notin\left[-1;1\right]\) ; \(f\left(-1\right)=-2\) ; \(f\left(1\right)=2\)
\(\Rightarrow-2\le f\left(t\right)\le2\Rightarrow-2\le m\le2\)
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình sau có ít nhất một nghiệm: sin x = x – 1 .
Chứng minh rằng phương trình cos2x = sinx − 2 có ít nhất hai nghiệm trong khoảng - π 6 ; π
Xét f(x) = cos2x - sinx + 2 trên các khoảng
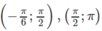
Đúng 0
Bình luận (0)
Chứng minh phương trình \(3x^4-3x^3-5x^2+2x+2=0\) có ít nhất 2 nghiệm nằm trong khoảng (-1;1)
Đặt \(f\left(x\right)=3x^4-3x^3-5x^2+2x+2\)
Hiển nhiên \(f\left(x\right)\) liên tục trên R cũng như mọi khoảng con của nó
\(f\left(-1\right)=1>0\)
\(f\left(-\dfrac{3}{4}\right)=-\dfrac{25}{256}< 0\)
\(f\left(0\right)=2>0\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(-1\right).f\left(-\dfrac{3}{4}\right)< 0\\f\left(-\dfrac{3}{4}\right).f\left(0\right)< 0\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 2 nghiệm thuộc (-1;0) nên có ít nhất 2 nghiệm thuộc (-1;1)
Đúng 0
Bình luận (0)
Chứng minh phương trình :
a) \(x^2-3x-7=0\) luôn có nghiệm
b) \(\cos2x=2\sin x-2\) có ít nhất hai nghiệm trong khoảng \(\left(-\dfrac{\pi}{6};\pi\right)\)
c) \(\sqrt{x^3+6x+1}-2=0\) có nghiệm dương
Cho phương trình :
\(\left(4-6m\right)sin^3x+3\left(2m-1\right)sinx+2\left(m-2\right)sin^2x.cosx-\left(4m-3\right)cosx=0\)
Tìm m để phương trình có nghiệm duy nhất \(x\in[0;\frac{\pi}{4}]\)
Chứng minh rằng phương trình: x 5 − 5 x – 1 = 0 có ít nhất ba nghiệm
Xét hàm số f ( x ) = x 5 − 5 x – 1 trên các đoạn [−2; −1], [−1; 0], [0; 3]
Đúng 0
Bình luận (0)
Chứng minh rằng phương trình: 2 x 3 – 6 x + 1 = 0 có ít nhất hai nghiệm
Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(0) = 1 > 0
f(1) = 2.13 – 6.1 + 1 = -3 < 0.
⇒ f(-2).f(0) < 0 và f(0).f(1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)
⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.
Đúng 0
Bình luận (0)
chứng minh rằng phương trình (m²-m+1)x⁴-2x³-1=0 có ít nhất 2 nghiệm /(-5;5)
Đặt \(f\left(x\right)=\left(m^2-m+1\right)x^4-3x^3-1\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên mọi khoảng trên R
\(f\left(0\right)=-1< 0\)
\(f\left(3\right)=81\left(m^2-m+1\right)-55=81\left(m-\dfrac{1}{2}\right)^2+\dfrac{23}{4}>0\)
\(\Rightarrow f\left(0\right).f\left(3\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(0;3\right)\)
\(f\left(-1\right)=m^2-m+2=\left(m-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Rightarrow f\left(-1\right).f\left(0\right)< 0\Rightarrow\) pt có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(\Rightarrow\) Pt có ít nhất 2 nghiệm thuộc \(\left(-1;3\right)\Rightarrow\) có ít nhất 2 nghiệm trên \(\left(-5;5\right)\)
Đúng 2
Bình luận (0)




