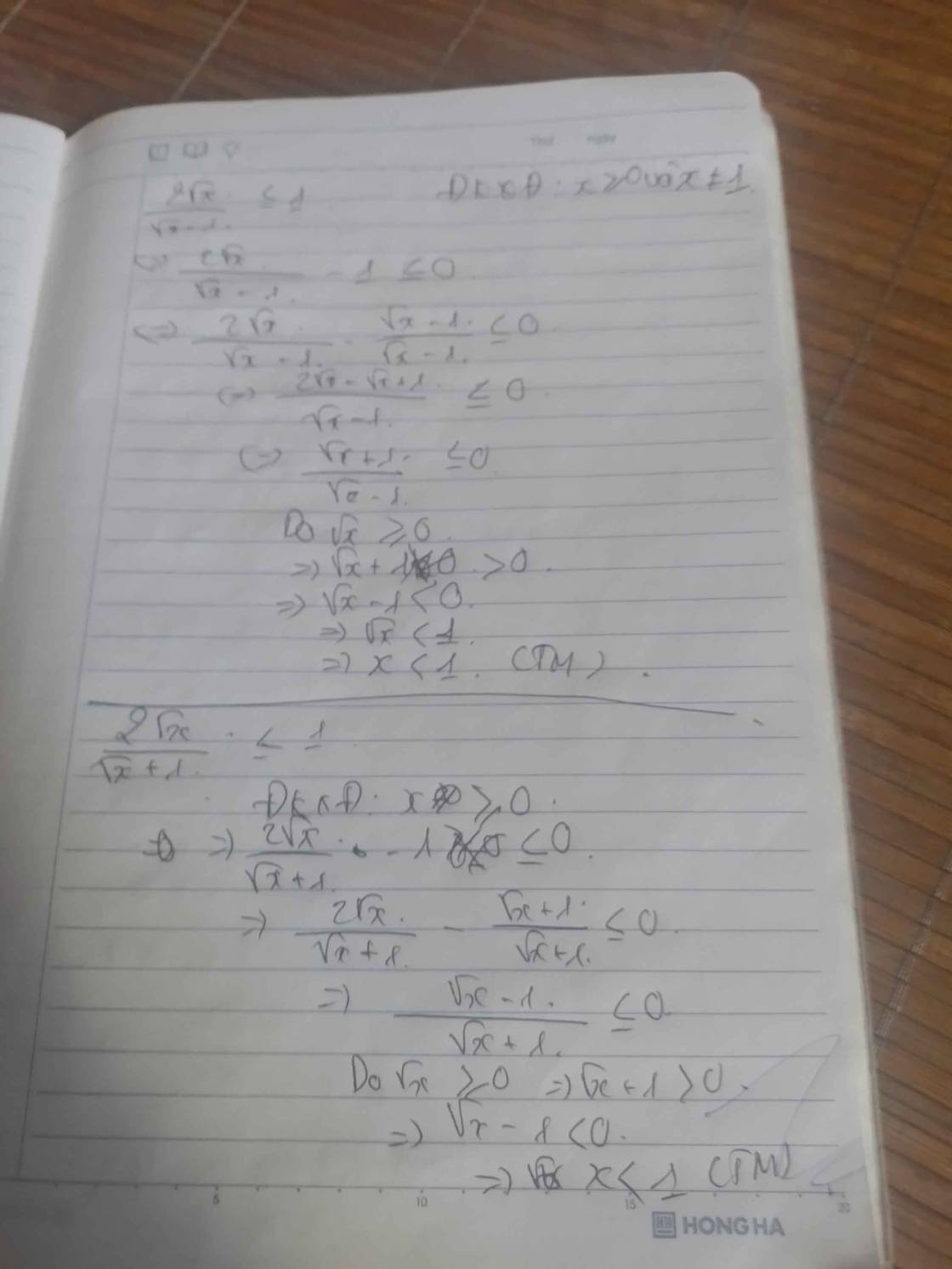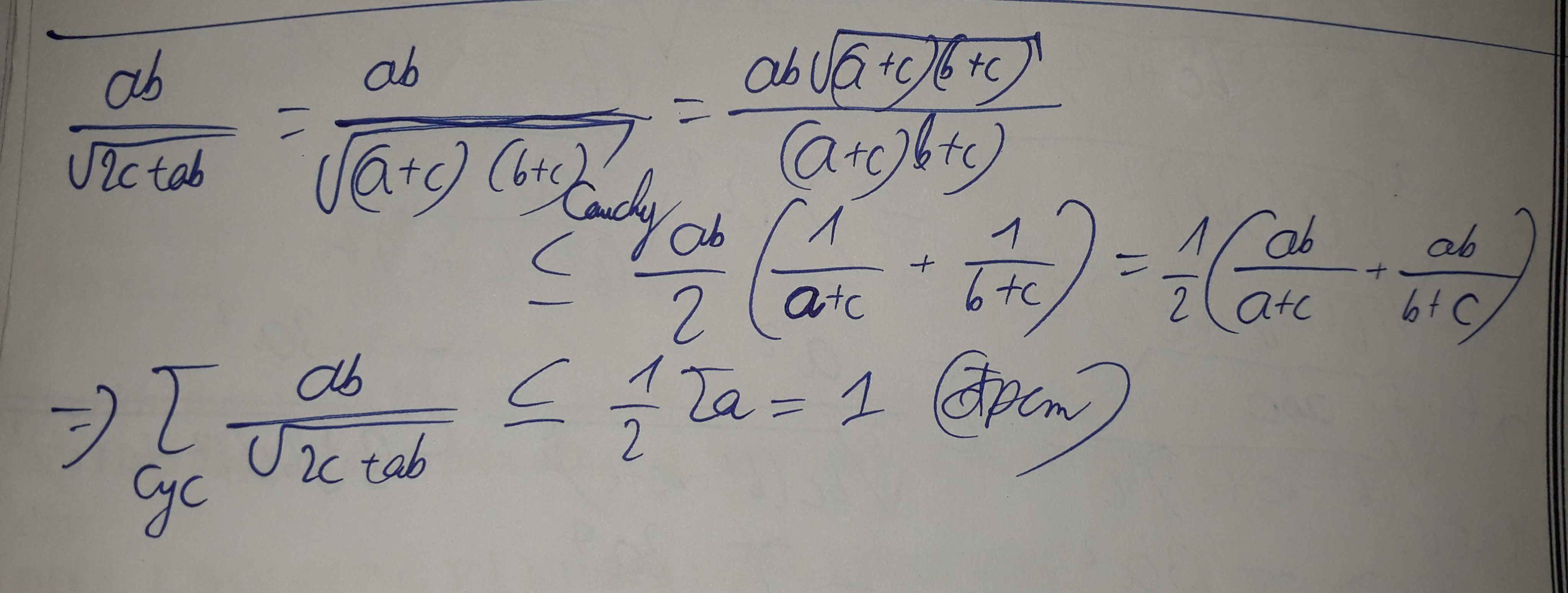\(\dfrac{2\sqrt{a}}{3}\le1\)
NS
Những câu hỏi liên quan
Tìm x để
a)\(\dfrac{2\sqrt{x}}{\sqrt{x}-1}\le1\)
b)\(\dfrac{2\sqrt{x}}{\sqrt{x}+1}\le1\)
Helppppp
P=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{8\sqrt{x}+8}{x+2\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}}\right):\left(\dfrac{x+\sqrt{x}+3}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}}\right)\)
a. rút gọn P
b. chứng minh rằng với mọi giá trị x ta luôn có P\(\le1\)
\(a,=\dfrac{x+8\sqrt{x}+8-\left(\sqrt{x+2}\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}:\dfrac{x+\sqrt{x}+3+\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+8\sqrt{x}+8-x-4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{2\sqrt{x}+x+5}\)
\(=\dfrac{4\sqrt{x}-4}{2\sqrt{x}+x+5}\)
Vậy \(P=\dfrac{4\sqrt{x}-4}{2\sqrt{x}+x+5}\)
Đúng 1
Bình luận (0)
Cho a,b,c>0 t/m \(a^2+b^2+c^2=1\).
C/m \(\dfrac{1}{4-\sqrt{ab}}+\dfrac{1}{4-\sqrt{bc}}+\dfrac{1}{4-\sqrt{ca}}\le1\)
Đề bài sai, bạn kiểm tra lại điều kiện \(a^2+b^2+c^2=1\)
Đúng 2
Bình luận (0)
Cho a, b, c > 0 và x + y + z = 3 .
CMR : \(\dfrac{x}{x+\sqrt{3x+yz}}+\dfrac{y}{y+\sqrt{3y+zx}}+\dfrac{z}{z+\sqrt{3z+xy}}\le1\)
Cho a,b,c >0 tm abc=1, C/m
\(\dfrac{1}{\sqrt{a^5+b^2+ab+6}}+\dfrac{1}{\sqrt{b^5+c^2+bc+6}}+\dfrac{1}{\sqrt{c^5+a^2+ca+6}}\le1\)
\(a^5+b^2+ab+6\ge3a^2b+6\)
\(\Rightarrow P\le\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{\sqrt{a^2b+2}}+\dfrac{1}{\sqrt{b^2c+2}}+\dfrac{1}{\sqrt{c^2a+2}}\right)\le\sqrt{\dfrac{1}{a^2b+2}+\dfrac{1}{b^2c+2}+\dfrac{1}{c^2a+2}}=\sqrt{Q}\)
\(Q=\dfrac{c}{a+2c}+\dfrac{a}{b+2a}+\dfrac{b}{c+2b}=\dfrac{1}{2}\left(1-\dfrac{a}{a+2c}+1-\dfrac{b}{b+2a}+1-\dfrac{c}{c+2b}\right)\)
\(Q=\dfrac{3}{2}-\dfrac{1}{2}\left(\dfrac{a^2}{a^2+2ac}+\dfrac{b^2}{b^2+2ab}+\dfrac{c^2}{c^2+2bc}\right)\)
\(Q\le\dfrac{3}{2}-\dfrac{1}{2}\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\)
\(\Rightarrow P\le\sqrt{1}=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Đúng 0
Bình luận (0)
a,b,c>0, a+b+c=2. CMR: \(\dfrac{a}{\sqrt{4a+3bc}}+\dfrac{b}{\sqrt{4b+3ac}}+\dfrac{c}{\sqrt{4c+3ab}}\le1\)
Ta có:
\(\left(\sqrt{a}.\dfrac{\sqrt{a}}{\sqrt{4a+3bc}}+\sqrt{b}\dfrac{\sqrt{b}}{\sqrt{4b+3ac}}+\sqrt{c}\dfrac{\sqrt{c}}{\sqrt{4c+3ab}}\right)^2\le\left(a+b+c\right)\left(\dfrac{a}{4a+3bc}+\dfrac{b}{4b+3ac}+\dfrac{c}{4c+3ab}\right)\)
\(=2\left(\dfrac{a}{4a+3bc}+\dfrac{b}{4b+3ac}+\dfrac{c}{4c+3ab}\right)\)
Nên ta chỉ cần chứng minh:
\(\dfrac{a}{4a+3bc}+\dfrac{b}{4b+3ac}+\dfrac{c}{4c+3ab}\le\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{4a}{4a+3bc}+\dfrac{4b}{4b+3ac}+\dfrac{4c}{4c+3ab}\le2\)
\(\Leftrightarrow\dfrac{3bc}{4a+3bc}+\dfrac{3ac}{4b+3ac}+\dfrac{3ab}{4c+3ab}\ge1\)
\(\Leftrightarrow\dfrac{bc}{4a+3bc}+\dfrac{ac}{4b+3ac}+\dfrac{ab}{4c+3ab}\ge\dfrac{1}{3}\)
Thật vậy, ta có:
\(VT=\dfrac{\left(bc\right)^2}{4abc+3\left(bc\right)^2}+\dfrac{\left(ca\right)^2}{4abc+3\left(ac\right)^2}+\dfrac{\left(ab\right)^2}{4abc+3\left(ab\right)^2}\)
\(VT\ge\dfrac{\left(ab+bc+ca\right)^2}{3\left(ab\right)^2+3\left(bc\right)^2+3\left(ca\right)^2+12abc}=\dfrac{\left(ab+bc+ca\right)^2}{3\left(ab\right)^2+3\left(bc\right)^2+3\left(ca\right)^2+6abc\left(a+b+c\right)}\)
\(VT\ge\dfrac{\left(ab+bc+ca\right)^2}{3\left(ab+bc+ca\right)^2}=\dfrac{1}{3}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=...\)
Đúng 1
Bình luận (0)
Cho ba số thực dương a, b, c thoả mãn a+b+c=2 Chứng minh rằng:
\(\dfrac{ab}{\sqrt{2c+ab}}+\dfrac{bc}{\sqrt{2a+bc}}+\dfrac{ca}{\sqrt{2b+ca}}\le1\)
\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Tìm m để phtrình \(3\sqrt{x-1}+m\sqrt{x+1}=2\sqrt[4]{x^2-1}\) có nghiệm
A. \(m\le\dfrac{1}{3}\) B. \(m\le1\) C. \(-1< m\le\dfrac{1}{3}\) D. \(-1\le m\le\dfrac{1}{3}\)
ĐKXĐ: \(x\ge1\)
\(3\sqrt[]{x-1}+m\sqrt[]{x+1}=2\sqrt[4]{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow3\sqrt[]{\dfrac{x-1}{x+1}}+m=2\sqrt[4]{\dfrac{x-1}{x+1}}\)
Đặt \(\sqrt[4]{\dfrac{x-1}{x+1}}=t\Rightarrow0\le t< 1\)
\(\Rightarrow3t^2+m=2t\Leftrightarrow-3t^2+2t=m\)
Xét \(f\left(t\right)=-3t^2+2t\) trên \([0;1)\)
\(f'\left(t\right)=-6t+2=0\Rightarrow t=\dfrac{1}{3}\)
\(f\left(0\right)=0;f\left(\dfrac{1}{3}\right)=\dfrac{1}{3};f\left(1\right)=-1\)
\(\Rightarrow-1< f\left(t\right)\le\dfrac{1}{3}\)
\(\Rightarrow-1< m\le\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
1/ Cho a,b>0 , thỏa mãn ab = 1. Chứng minh rằng:
\(\dfrac{a}{\sqrt{b+2}}+\dfrac{b}{\sqrt{a+2}}+\dfrac{1}{\sqrt{a+b+ab}}\ge\sqrt{3}\)
2/ Cho a>0. Chứng minh rằng:
a+\(\dfrac{1}{a}\ge\sqrt{\dfrac{1}{a^2+1}}+\sqrt{1+\dfrac{1}{a^2+1}}\)
3/ Cho a, b>0. Chứng minh rằng:
2(a+b)\(\le1+\sqrt{1+4\left(a^3+b^3\right)}\)