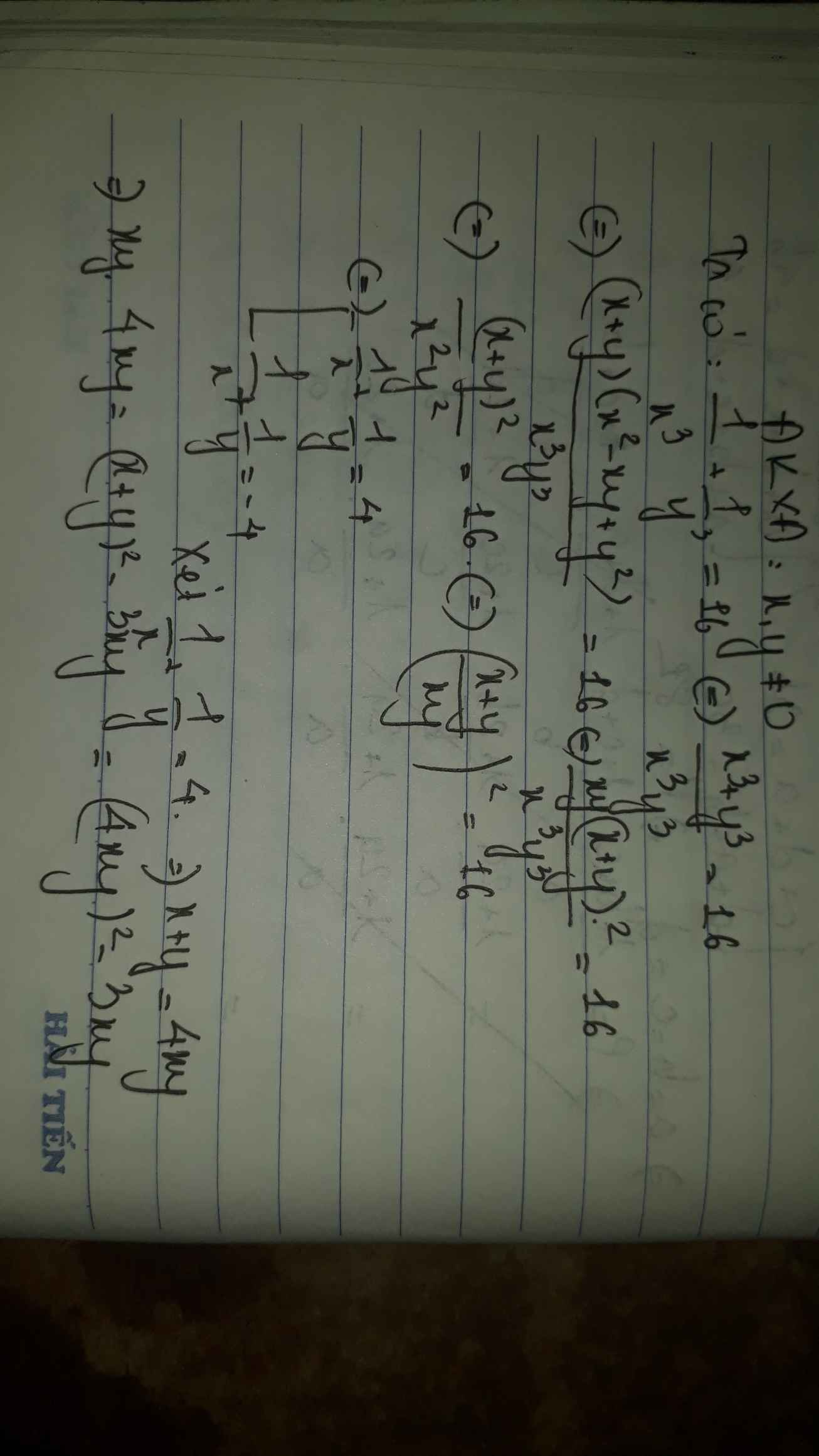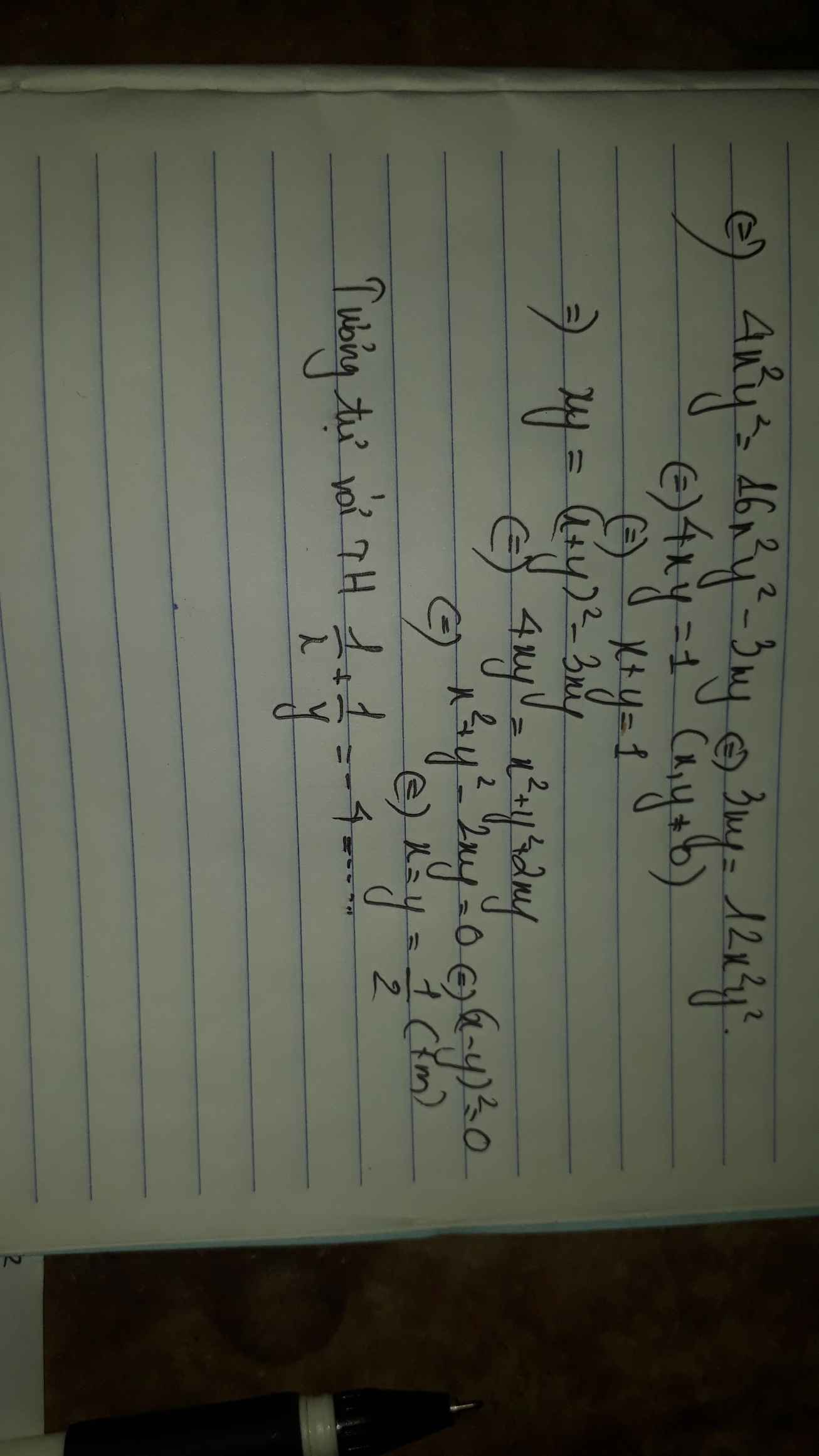TH
Những câu hỏi liên quan
Giải hệ pt;
\(\left\{{}\begin{matrix}xy\left(x+y\right)=x^2-xy+y^2\\\dfrac{1}{x^3}+\dfrac{1}{y^3}=16\end{matrix}\right.\)
giải hệ pt: xy=120
xy=(x+10)(y-1)
\(\left\{{}\begin{matrix}xy=120\\xy=\left(x+10\right)\left(y-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=120\\xy=xy-x+10y-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=120\\x=10y-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(10y-10\right)y=120\\x=10y-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y^2-y-12=0\\x=10y-10\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=4\Rightarrow x=30\\y=-3\Rightarrow x=-40\end{matrix}\right.\)
Đúng 2
Bình luận (0)
1/ giải pt, và hệ sau:
a/ √(x-2) + √(10-x) = x^2 -12x +40
b/ hệ:#1/x + 1/y + 1/z =2
#2/xy - 1/z^2 = 4
2/ tìm các số x, y, z thỏa hệ:
#1/x +16/y +9/z = 4
#x+y+z =< 16
3/ Tìm GTLN và GTNN của biển thức:
A= 3√(x-1) + 4√(5-x)
giải hệ pt \(\left\{{}\begin{matrix}x+xy+y=2\\x^2+xy+y^2=4\end{matrix}\right.\)
Cộng vế với vế:
\(x^2+2xy+y^2+x+y=6\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+y\right)-6=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=-3\\x+y=2\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+y=-3\\xy=5\end{matrix}\right.\)
Theo Viet đảo, x và y là nghiệm của:
\(t^2+3t+5=0\) (vô nghiệm)
TH2: \(\left\{{}\begin{matrix}x+y=2\\xy=0\end{matrix}\right.\)
Theo Viet đảo, x và y là nghiệm:
\(t^2-2t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=2\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)=\left(2;0\right);\left(0;2\right)\)
Đúng 1
Bình luận (0)
giải hệ pt
\(\hept{\begin{cases}\left(x-y\right)\left(x^2+xy+y^2+3\right)=3\left(x^2+y^2\right)+2\\4\sqrt{x+2}+\sqrt{16-3y}=x^2+8\end{cases}}\)
PT 1 \(\Leftrightarrow x-y.x^2+xy+y^2+3.x-y-3x^2+y^2-2=0\)
\(\Leftrightarrow x^3-3x^3+3x-1=y^3+3y^3+3y+1\)
\(\Leftrightarrow x-1^3=x+1^3\)
\(\Leftrightarrow x-y-2=0\)
Thay vào PT 2 nhân liên hợp.
PT 1 suy ra \(y=x-2\)thay vào PT 2, ta có:
\(4\sqrt{x+2}+\sqrt{22-3x}=x^2+8\)\(-2\le x\le\frac{22}{3}\)
\(\Leftrightarrow4.\sqrt{x+2}-2+\sqrt{22-3x}-4=x^2-4\)
\(\Leftrightarrow x-2.x+2+\frac{3}{\sqrt{22-3x}+4}-\frac{4}{\sqrt{x+2}+2}=0\)
TH1:x=2 thay vào (1) suy ra y=0
TH2: f(x)= \(x+2+\frac{3}{\sqrt{22-3x}+4}-\frac{4}{\sqrt{x+2}+2}=0\)*
ta thấy x=-1 là 1 nghiệm của PT(*)
NHận xét rằng giả xử có số a thoả \(-2\le x\le a\le\frac{22}{3}\)
Ta có: \(\sqrt{x+2}< \sqrt{a+2};\sqrt{22-3x}>\sqrt{22-3a}\)
\(\Rightarrow-\frac{4}{\sqrt{x+2}+2}< -\frac{4}{\sqrt{a+2}+2}\)
\(\frac{3}{\sqrt{22-3x}+4}< \frac{3}{\sqrt{22-3a}+4}\)
Suy ra f(x)<< f(a) suy hàm f(x) đồng biến
suy x=-1 thì f(x)=0
x<-1 thì f(x) <0
x>-1 thì f(x)>0
suy ra x=-1 là nghiệm duy nhất của(*)
thay vào (1) ta có y=-3
P/s: Tôi ko chắc, mới lớp 6 thôi
Đúng 0
Bình luận (0)
Giải hệ pt sau :
\(\left\{{}\begin{matrix}\left(x-10\right)\left(y+\frac{4}{5}\right)=xy\\\left(x-20\right)\left(y+2\right)=xy\end{matrix}\right.\)
https://i.imgur.com/staosTs.jpg
Giải hệ pt sau:
X-y =2 và
2x bình - xy + y bình =4
Xem chi tiết
bạn ê làm bài gì trong lhó thế
giải ra x=1,y-1 Nhưng viết trên đây khó quá @_@
giải hệ phương trình \(\hept{\begin{cases}\sqrt{x}+\sqrt{y}+4\sqrt{xy}=16\\x+y=10\end{cases}}\)
đk: \(x,y\ge0\)
Đặt \(\hept{\begin{cases}\sqrt{x}+\sqrt{y}=a\\\sqrt{xy}=b\end{cases}}\) với \(a,b\ge0\)
\(\Rightarrow x+y=\left(\sqrt{x}+\sqrt{y}\right)^2-2\sqrt{xy}=a^2-2b\)
Khi đó \(HPT\Leftrightarrow\hept{\begin{cases}a+4b=16\\a^2-2b=10\end{cases}}\)
Đến đây thì dễ dàng rồi: \(HPT\Leftrightarrow\hept{\begin{cases}b=\frac{16-a}{4}\\a^2-2b=10\end{cases}}\)
\(\Leftrightarrow a^2-\frac{16-a}{2}=10\)
\(\Leftrightarrow2a^2+a-36=0\)
\(\Leftrightarrow\left(2a^2-8a\right)+\left(9a-36\right)=0\)
\(\Leftrightarrow\left(a-4\right)\left(2a+9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=4\\a=-\frac{9}{2}\left(ktm\right)\end{cases}}\Rightarrow\hept{\begin{cases}a=4\\b=\frac{16-4}{4}=3\end{cases}}\)
Gọi \(\sqrt{x},\sqrt{y}\) là 2 nghiệm của PT \(t^2-4t+3=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-3\right)=0\Leftrightarrow\orbr{\begin{cases}t=1\\t=3\end{cases}}\Leftrightarrow\left(\sqrt{x};\sqrt{y}\right)\in\left\{\left(1;3\right);\left(3;1\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;9\right);\left(9;1\right)\right\}\)
Giải các hệ pt và các pt sau:
1. (x+1)(y-1)=xy+4 (1)
(2x-4)(y+1)=2xy+5(2)
2. \(x^2+x-2\sqrt{x^2+x+1}+2=0\)
1.
HPT \(\left\{\begin{matrix} (x+1)(y-1)=xy+4\\ (2x-4)(y+1)=2xy+5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} xy-x+y-1=xy+4\\ 2xy+2x-4y-4=2xy+5\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} -x+y=5\\ 2x-4y=9\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} x=\frac{-29}{2}\\ y=\frac{-19}{2}\end{matrix}\right.\)
Vậy.............
Đúng 1
Bình luận (0)
2.
ĐKXĐ: $x\in\mathbb{R}$
$x^2+x-2\sqrt{x^2+x+1}+2=0$
$\Leftrightarrow (x^2+x+1)-2\sqrt{x^2+x+1}+1=0$
$\Leftrightarrow (\sqrt{x^2+x+1}-1)^2=0$
$\Rightarrow \sqrt{x^2+x+1}=1$
$\Rightarrow x^2+x=0$
$\Leftrightarrow x(x+1)=0$
$\Rightarrow x=0$ hoặc $x=-1$
Đúng 1
Bình luận (0)