C/m với mọi x,y>0
\(\left(1+x^2\right)\left(1+y^2\right)\ge\left(x+y\right)\left(1+xy\right)\)
Với mọi x,y>0 c/m: \(\left(x^2+y^2\right)\sqrt{x^2+y^2}\ge\sqrt{2}xy\left(x+y\right)\)
Ta có: \(x^2+y^2\ge2xy\)
\(\sqrt{x^2+y^2}\ge\sqrt{\frac{\left(x+y\right)^2}{2}}=\frac{\sqrt{2}}{2}\left(x+y\right)\)
Do các vế của BĐT đều dương, nhân vế với vế:
\(\left(x^2+y^2\right)\sqrt{x^2+y^2}\ge\sqrt{2}xy\left(x+y\right)\) (đpcm)
Dấu "=" xảy ra khi \(x=y\)
Mọi người ơi giúp mình với
Câu 1: Cho x, y, z > 0 và \(5\left(x^2+y^2+z^2\right)=6\left(xy+yz+xz\right)\)Tìm giá trị nhỏ nhất của
\(P=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)
Câu 2: Cho a, b, c >0 và \(\left\{{}\begin{matrix}ab+bc+ca>0\\a\ge c\end{matrix}\right.\)Tìm giá trị nhỏ nhất của
\(p=\frac{\left(a+b\right)}{\left(b+c\right)}+\frac{\left(b+c\right)}{\left(c+a\right)}+\frac{\left(c+a\right)^2}{a\left(b+c\right)+c\left(b+a\right)}\)
1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
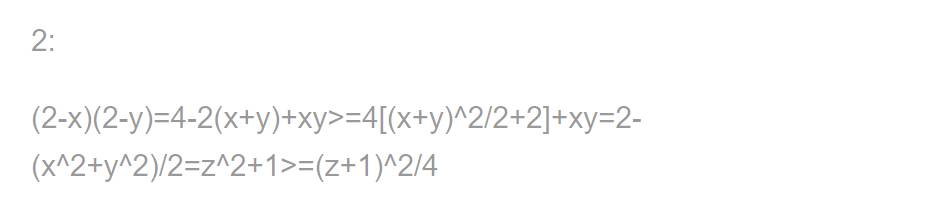
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Cho x;y>0
CMR: \(\dfrac{\left(x^3+8\right)\left(y^2-y+1\right)}{\left(x^2+x\right)\left(xy^2+2\right)}\ge\dfrac{1}{2}\)
Cho x;y>0
CMR: \(\frac{\left(x^3+8\right)\left(y^2-y+1\right)}{\left(x^2+x\right)\left(xy^2+2\right)}\ge\frac{1}{2}\)
GIÚP MÌNH GIẢI BÀI NÀY VỚI !!!
a \(\left(x-1\right)^2-\left(y+1\right)^2=0\)
\(x+3y-5=0\)
b \(xy-2x-y+2=0\)
3x+y=8
c \(\left(x+y\right)^2-4\left(x+y\right)=12\)
\(\left(x-y\right)^2-2\left(x-y\right)=3\)
d \(2x-y=1\)
\(2x^2+xy-y^2-3y=-1\)
a.
\(\left\{{}\begin{matrix}\left(x-1\right)^2-\left(y+1\right)^2=0\\x+3y-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1-y-1\right)\left(x-1+y+1\right)=0\\x+3y-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y-2\right)\left(x+y\right)=0\\x+3y-5=0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x-y-2=0\\x+3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{4}\\y=\dfrac{3}{4}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x+y=0\\x+3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=\dfrac{5}{2}\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}xy-2x-y+2=0\\3x+y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(y-2\right)-\left(y-2\right)=0\\3x+y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(y-2\right)=0\\3x+y=8\end{matrix}\right.\)
TH1:
\(\left\{{}\begin{matrix}x-1=0\\3x+y=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
TH2:
\(\left\{{}\begin{matrix}y-2=0\\3x+y=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
c.
\(\left\{{}\begin{matrix}\left(x+y\right)^2-4\left(x+y\right)-12=0\\\left(x-y\right)^2-2\left(x-y\right)=3\end{matrix}\right.\)
Xét pt:
\(\left(x+y\right)^2-4\left(x+y\right)-12=0\)
\(\Leftrightarrow\left(x+y+2\right)\left(x+y-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y+2=0\\x+y-6=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-x-2\\y=6-x\end{matrix}\right.\)
TH1: \(y=-x-2\) thế vào \(\left(x-y\right)^2-2\left(x-y\right)=3\)
\(\Rightarrow\left(2x+2\right)^2-2\left(2x+2\right)=3\)
\(\Leftrightarrow4x^2+4x-3=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\Rightarrow y=-\dfrac{5}{2}\\x=-\dfrac{3}{2}\Rightarrow y=-\dfrac{1}{2}\end{matrix}\right.\)
TH2: \(y=6-x\) thế vào...
\(\left(2x-6\right)^2-2\left(2x-6\right)=3\)
\(\Leftrightarrow4x^2-28x+45=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\Rightarrow y=\dfrac{7}{2}\\y=\dfrac{9}{2}\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Chứng minh với mọi x, y \(\in R\), bất đẳng thức sau luôn đúng:
\(\left(x+y\right)^2+1-xy\ge\sqrt{3}\left(x+y\right)\)
Dễ thấy:
\(VT\ge\left(x+y\right)^2+1-\dfrac{\left(x+y\right)^2}{4}=\dfrac{3\left(x+y\right)^2}{4}+1\)
Áp dụng Cô-si:
\(\dfrac{3\left(x+y\right)^2}{4}+1\ge2\sqrt{\dfrac{3\left(x+y\right)^2}{4}.1}=\sqrt{3}\left|x+y\right|\ge\sqrt{3}\left(x+y\right)\)
Do đó:
\(\left(x+y\right)^2+1-xy\ge\sqrt{3}\left(x+y\right),\forall x,y\in R\)
Cho x,y,z>0. CM: \(\dfrac{xy}{z^2\left(x+y\right)}+\dfrac{yz}{x^2\left(y+z\right)}+\dfrac{zx}{y^2\left(z+x\right)}\ge\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
\(VT=\dfrac{\left(\dfrac{1}{z}\right)^2}{\dfrac{1}{x}+\dfrac{1}{y}}+\dfrac{\left(\dfrac{1}{x}\right)^2}{\dfrac{1}{y}+\dfrac{1}{z}}+\dfrac{\left(\dfrac{1}{y}\right)^2}{\dfrac{1}{x}+\dfrac{1}{z}}\ge\dfrac{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}{2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
Dâu "=" xảy ra khi \(x=y=z\)
Cho x, y, z >0 thoả mãn \(x^2+y^2+z^2=1\) . Cmr: \(\frac{x+y+z}{xy+yz+xz}\ge\sqrt{3}+\frac{1}{2\sqrt{3}}\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\)