Tam giác DEF vuông tại D có DF=10cm,gốc E=60°. Tính: Gốc F; DE; EF
H24
Những câu hỏi liên quan
Tam giác DEF vuông tại D , có Góc E=60 độ , EF=15 tính DE , DF
Xét ΔDEF vuông tại D có
\(DE=DF\cdot\cos60^0\)
\(=15\cdot\dfrac{1}{2}=7.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDFE vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow DF^2=15^2-7.5^2=\dfrac{675}{4}\)
hay \(DF=\dfrac{15\sqrt{3}}{2}\left(cm\right)\)
Đúng 1
Bình luận (0)
Tam giác DEF vuông tại D , có Góc E=60 độ , EF=15 tính DE , DF
DE=cos E .EF
DE=0,5.15
DE=7,5cm
DF=sinE.EF
DF=\(\dfrac{\sqrt{3}}{2}.15=\dfrac{15\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
Ta có: \(\cos60^o=\dfrac{DE}{E\text{F}}=\dfrac{\text{1}}{2}\Rightarrow DE=\dfrac{E\text{F}}{2}=\dfrac{\text{1}5}{2}=7,5cm\)
Áp dụng định lí Py-ta-go vào ΔDEF vuông tại D
⇒ EF2=DE2+DF2 ⇒ DF2=EF2-DE2=152-7,52=168,75
⇒ \(DF=\dfrac{15\sqrt{3}}{2}\) cm
Đúng 0
Bình luận (0)
Xét ΔDEF vuông tại D có
\(DE=DF\cdot\cos60^0\)
\(=15\cdot\dfrac{1}{2}\)
=7,5(cm)
Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(FE^2=DF^2+DE^2\)
\(\Leftrightarrow DF^2=168.75\)
hay \(DF=\dfrac{15\sqrt{3}}{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác def vuông tại d và đường cao dh. M,n lần lượt là trung điểm cua đe và df. Tính gốc mhn
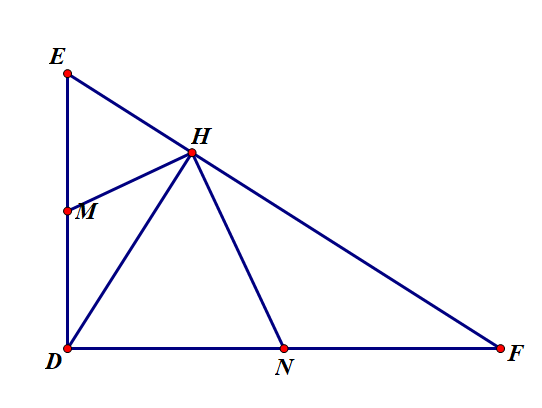
\(\text{Xét tam giác EHD vuông tại H có đường trung tuyến HM ứng với cạnh huyền ED}\)
\(\Rightarrow MH=MD=ME=\dfrac{1}{2}ED\)
\(\Rightarrow\)Tam giác HMD cân tại M
\(\Rightarrow\)\(\widehat{MHD}=\widehat{MDH}\)
Tương tự với tam giác DHF vuông tại H ta được \(\widehat{DHN}=\widehat{HDN}\)
Ta có \(\widehat{MHN}=\widehat{MHD}+\widehat{NHD}=\widehat{MDH}+\widehat{NDH}=\widehat{MDN}\)
Suy ra góc MHN có số đo 90 độ
Tick nha bạn 😘
Đúng 3
Bình luận (2)
Ta có: ΔDHE vuông tại H(Gt)
mà HM là đường trung tuyến ứng với cạnh huyền DE(Gt)
nên HM=DM=ME
Ta có: ΔDHF vuông tại H(gt)
mà HN là đường trung tuyến ứng với cạnh huyền DF(Gt)
nên HN=DN=FN
Xét ΔNDM và ΔNHM có
ND=NH(cmt)
NM chung
MD=MH(cmt)
Do đó: ΔNDM=ΔNHM(c-c-c)
Suy ra: \(\widehat{NDM}=\widehat{NHM}\)
hay \(\widehat{NHM}=90^0\)
Đúng 0
Bình luận (0)
Cho tam giác DEF biết DE = 6 cm, DF = 8 cm, EF = 10cm.
a) Cmr : Tam giác DEF là tam giác vuông
b) Vẽ DK là đường cao. Tính DK và FK
c) Giải tam giác EDK
d) Vẽ phân giác trong EM của góc DEF. Tính MD, MF, ME.
e) Tính sin F trong các tam giác vuông DFK và DEF. Từ đó suy ra : ED . DF = DK . EF
a: Xét ΔDEF có \(EF^2=DE^2+DF^2\)
nên ΔDEF vuông tại D
Đúng 1
Bình luận (0)
Cho tam giác DEF vuông tại D, EF=10cm; DE+DF=14cm; DE<DF. Tính chu vi, diện tích tam giác DEF.
Cho tam giác DEF có EF = 10cm, DE=6cm, DF=8cm. DH vuông góc với F tại M a)CMR: Tam giác DEF vuông b)Tính DH, HE, HI c)Gọi I là trung điểm DF vẽ IM vuông góc với EF CMR: DE2=ME2-MF2
Cho tam giác abc vuông tại A. Vẽ phân giác BD của góc ABC(D€AC),đường thẳng qua D và vuông gốc với BC cắt BC tại E và cắt AB tại F.
a. Cm DF >DE và BD vuông gốc vs FC
b. Hạ AH vuôg gốc BC (H€BC). Cm AB^2+HC^2=AC^2+BH^2
Cho tam giác DEF vuông tại D có đường cao DH, DE=15cm, DF=20cm
a) Tính EF,DH,EH,HF
b) Tính so đo góc E, góc F
\(a,\) Áp dụng Pytago \(EF=\sqrt{DE^2+DF^2}=25\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}DE^2=EH\cdot EF\\DF^2=FH\cdot EF\\DH^2=FH\cdot EH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}EH=\dfrac{DE^2}{EF}=9\left(cm\right)\\FH=\dfrac{DF^2}{EF}=16\left(cm\right)\\DH=\sqrt{9\cdot16}=12\left(cm\right)\end{matrix}\right.\)
\(b,\sin\widehat{E}=\cos\widehat{F}=\dfrac{DF}{EF}=\dfrac{4}{5}\approx\left\{{}\begin{matrix}\sin53^0\\\cos37^0\end{matrix}\right.\\ \Rightarrow\widehat{E}\approx53^0;\widehat{F}\approx37^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm , BC = 10cm và tam giác DEF vuông tại D có DE = 9cm, DF = 12cm, EF = 15cm.
a) Hai tam giác ABC và DEF có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác ấy?
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)




