MÌNH CẦN GẤPPPPPPPPPPPPPPPPPPPPPPPP CÂU B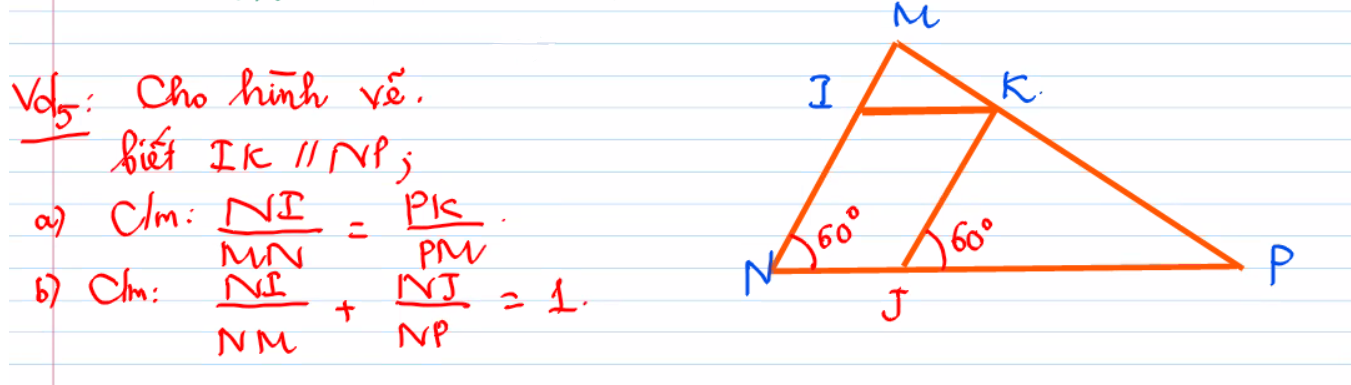
CI
Những câu hỏi liên quan
Answer the questions using ''too''
Why can't elephants jump?
Cần gấpppppppppppppppppppppppp
1 Elephants cam't jump because they're too fat.
Tính giá trị biểu thức
A= 99-97+95-9+91-89+.....+7-5+3-1
NHANH CẦN RẤT GẤPPPPPPPPPPPPPPPPPPPPPPPP
A=99-97+...+7-5+3-1
=[99-97]+..+[7-5]+[3-1]
=2+...+2+2
=2*50
100
Đúng 0
Bình luận (0)
A=99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1
Ta thấy khoảng cách giữa 2 số liên tiếp là 2
-> Số lượng số hạng của dãy là :(99-1)/2 + 1 =50
Mà cứ 2 số là 1 cặp => có 50/2 =25 cặp tất cả
Vậy A=99 - 97 + 95 - 93 + 91 - 89 + ... + 7 - 5 + 3 - 1
= (99-97)+(95-93)+(91-89)+.....+(7-5)+(3-1)
= 2*25
=50
Đúng 0
Bình luận (0)
A= 99-97+95-93+91-89+.....+7-5+3-1
A = 2 + 2 + 2 + 2 +.... + 2 ( có 50 số 2 )
=> A = 2 . 50 = 100
Vậy A = 100
Study well
Đúng 0
Bình luận (0)
người thợ may cắt 12,5% chiều dài tấm vải được 3m vải. Hỏi cả tấm vải ban đầu dài bao nhiêu mét?
gấpppppppppppppppppppppppp
mik tick cho
Cả tấm vải ban đầu dài số m là:
3:12,5%=24(m)
đ/s
Ban đầu cả tấm vải dài: 3:12.5%=24 (m)
Đáp số: 24 m
Chiều dài của tấm vải ban đầu là:
3 : 12,5 % = 24 (m ) [ Nếu không quen thì bạn có thể viết: 3 : 12,5 x 100 = 24 m]
Đáp số: 24 m
Xem thêm câu trả lời
tìm tất cả các số tự nhiên có 3 chữ số , biết rằng số đó chia hết cho 6 và chữ số hàng chục chia cho chữ số hàng đơn vị được thương là 2 dư 1 gấpppppppppppppppppppppppp
Goi số cần tìm là abc . Để abc chia hết cho 6 thì abc phải là số chia hết cho 2 và 3 => abc phải là số chẵn và (a + b + c) chia hết cho 3
Theo đề bài chữ số hàng chục = 2 lần chữ số hàng đơn vị +1 và chữ số hàng chục phải <=9
=> Chữ số hàng đơn vị chỉ có thể là 2 hoặc 4
+ Với chữ số hàng đv = 2 => chữ số hàng chục là 2x2+1=5 => abc = a52 => a = 2 hoặc a = 5 hoặc a = 8 để a52 chia hết cho 3
Vậy số cần tìm là các số: 252; 552; 852 thỏa mãn đề bài
+ Với chữ số hàng đv = 4 => chữ số hàng chục là 2x4+1=9 => abc = a94 => a = 2 hoặc a=5 hoặc a=8 để a94 chia hết cho 3
Vậy số cần tìm là các số: 294; 594; 894
Đúng 0
Bình luận (0)
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình câu b với mình cần gấp 
b: \(A=\dfrac{\sqrt{x}-\sqrt{x}+1}{x-1}\cdot\dfrac{x-1}{\sqrt{x}-1}=\dfrac{1}{\sqrt{x}-1}\)
Đúng 1
Bình luận (0)
Mình đang cần câu b và câu c ạ
Tứ giác AOKC nội tiếp (K và A cùng nhìn OC dưới góc vuông)
\(\Rightarrow\widehat{ACO}=\widehat{AKO}\) (cùng chắn AO) (1)
Mà \(\widehat{ACO}=\widehat{IAO}\) (cùng phụ \(\widehat{AOC}\)) (2)
\(\widehat{IAO}=\widehat{OIA}\) (\(OI=OA\) nên tam giác OIA cân tại O) (3)
(1);(2);(3) \(\Rightarrow\widehat{OIA}=\widehat{AKO}\)
Do \(\widehat{OIA}\) và \(\widehat{AKO}\) cùng chắn OA \(\Rightarrow OKIA\) nội tiếp
c. Theo cmt \(\Rightarrow\widehat{AIK}+\widehat{AOK}=180^0\)
AOKC nội tiếp (như đầu câu b đã nói) \(\Rightarrow\widehat{AOK}+\widehat{ACK}=180^0\)
\(\Rightarrow\widehat{AIK}=\widehat{ACK}\) (4)
Lại có tứ giác ACDH nội tiếp (D và H cùng nhìn AC dưới 1 góc vuông)
\(\Rightarrow\widehat{ACK}+\widehat{AHD}=180^0\) mà \(\widehat{AHD}+\widehat{MHD}=180^0\Rightarrow\widehat{ACK}=\widehat{MDH}\) (5)
(4);(5) \(\Rightarrow\widehat{AIK}=\widehat{MHD}\Rightarrow DH||IK\) (2 góc so le trong bằng nhau)
\(\Rightarrow\dfrac{DM}{KM}=\dfrac{HM}{IM}\) (định lý Talet)
Mặt khác \(CH||IB\) (cùng vuông góc AB)
\(\Rightarrow\dfrac{CM}{BM}=\dfrac{HM}{IM}\)
\(\Rightarrow\dfrac{DM}{KM}=\dfrac{CM}{BM}\Rightarrow DM.BM=KM.CM\)
Đúng 1
Bình luận (0)
tưởng anh Thịnh lên c3 rồi chứ
Đúng 0
Bình luận (2)
Mình cần câu b
Lời giải:
Đặt $\sqrt{x}=a(a\geq 0)$ thì pt trở thành:
$a^4+2a^3-5a^2-4a+6=0$
$\Leftrightarrow (a^4+2a^3+a^2)-6a^2-4a+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)-2a^2+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)+4-2(a^2-1)=0$
$\Leftrightarrow (a^2+a-2)^2-2(a^2-1)=0$
$\Leftrightarrow (a+2)^2(a-1)^2-2(a-1)(a+1)=0$
$\Leftrightarrow (a-1)[(a+2)^2(a-1)-2(a+1)]=0$
$\Leftrightarrow (a-1)(a^3+3a^2-2a-6)=0$
$\Leftrightarrow (a-1)[a^2(a+3)-2(a+3)]=0$
$\Leftrightarrow (a-1)(a+3)(a^2-2)=0$
$\Rightarrow a=1$ hoặc $a=\sqrt{2}$ (do $a\geq 0$)
$\Leftrightarrow x=1$ hoặc $x=2$
Đúng 2
Bình luận (0)
Lời giải:
Đặt $\sqrt{x}=a(a\geq 0)$ thì pt trở thành:
$a^4+2a^3-5a^2-4a+6=0$
$\Leftrightarrow (a^4+2a^3+a^2)-6a^2-4a+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)-2a^2+6=0$
$\Leftrightarrow (a^2+a)^2-4(a^2+a)+4-2(a^2-1)=0$
$\Leftrightarrow (a^2+a-2)^2-2(a^2-1)=0$
$\Leftrightarrow (a+2)^2(a-1)^2-2(a-1)(a+1)=0$
$\Leftrightarrow (a-1)[(a+2)^2(a-1)-2(a+1)]=0$
$\Leftrightarrow (a-1)(a^3+3a^2-2a-6)=0$
$\Leftrightarrow (a-1)[a^2(a+3)-2(a+3)]=0$
$\Leftrightarrow (a-1)(a+3)(a^2-2)=0$
$\Rightarrow a=1$ hoặc $a=\sqrt{2}$ (do $a\geq 0$)
$\Leftrightarrow x=1$ hoặc $x=2$
mình cần câu b

a: PTHĐGĐ là:
x^2-2mx-3=0
a*c=1*(-3)=-3<0
=>(d) luôn cắt (P) tại hai điểm phân biệt
b:
Giả sử x1>0; x2<0
|x1|+3|x2|=6
=>|x1|-|x2|(x1x2)=6
=>x1+x2(x1x2)=6
=>x1-3x2=6
mà x1+x2=2m
nên -4x2=6-2m
=>x2=1/2m-3/2
=>x1=6+3/2m-9/2=3/2m+3/2
x1*x2=-3
=>(1/2m-3/2)(3/2m+3/2)=-3
=>(m-3)(m+1)*3/2*1/2=-3
=>(m^2-2m-3)=-3:3/4=-4
=>m^2-2m+1=0
=>m=1
Đúng 0
Bình luận (0)




