Mình cần giúp đỡ mình cũng không biết bài này thuộc bài nào nên để đại ạ(◕ᴗ◕✿)
MH
Những câu hỏi liên quan
Ai giúp mình bài văn tả cồng vòng với ạ. Cho mk cảm ơn trc ạ. (*•̀ᴗ•́*)و ̑̑
Mình cần gấp nên mong mn giúp nhiệt tình ạ🥲
Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Vì mình ko biết gõ ra thành chữ nên chỉ có hình,mọi người thông cảm ạ!
Mọi người giúp mình giải bài này nhé, càng chi tiết càng tốt ạ
Mình đang cần gấp
Cảm ơn mọi người đã giúp đỡ ạ
Đọc tiếp
 Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Đề bài: Trục căn thức ở mẫu và rút gọn (nếu được)
Vì mình ko biết gõ ra thành chữ nên chỉ có hình,mọi người thông cảm ạ!
Mọi người giúp mình giải bài này nhé, càng chi tiết càng tốt ạ
Mình đang cần gấp
Cảm ơn mọi người đã giúp đỡ ạ
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
Đúng 2
Bình luận (0)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
Đúng 2
Bình luận (0)
\(\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}\)
= \(\dfrac{2.\left(\sqrt{6}+2\right)+2\left(\sqrt{6}-4\right)}{\left(\sqrt{6}-2\right)}\) + \(\dfrac{5}{\sqrt{6}}\)
= \(\dfrac{2\sqrt{6}+4+2\sqrt{6}-4}{6-4}\) + \(\dfrac{5\sqrt{6}}{6}\)
= \(\dfrac{4\sqrt{6}}{2}\) + \(\dfrac{5\sqrt{6}}{6}\)
= \(\dfrac{12\sqrt{6}+5\sqrt{6}}{6}\)
= \(\dfrac{17\sqrt{6}}{6}\)
Đúng 1
Bình luận (0)
Tìm x:x+frac{x}{x+1}+frac{x+3}{x^2+5x+6}+frac{x+4}{x^2+6x+8}-10Giúp mình với, bài Violympic á. Cảm ơn các bạnÀ bài này mình cũng thấy khó nên bạn nào thấy khó mà giải ko được thì ko cần comment nha. Còn bạn nào không biết làm thì cũng không sao, vì bài này khó mà, miễn là đừng comment những khác ngoài đáp án của bạn cho mình là được. Cảm ơn thời gian và công sức của các bạn để giúp mình, chúc các bạn một ngày tốt lành.
Đọc tiếp
Tìm x:
\(x+\frac{x}{x+1}+\frac{x+3}{x^2+5x+6}+\frac{x+4}{x^2+6x+8}-1=0\)
Giúp mình với, bài Violympic á. Cảm ơn các bạn
À bài này mình cũng thấy khó nên bạn nào thấy khó mà giải ko được thì ko cần comment nha. Còn bạn nào không biết làm thì cũng không sao, vì bài này khó mà, miễn là đừng comment những khác ngoài đáp án của bạn cho mình là được. Cảm ơn thời gian và công sức của các bạn để giúp mình, chúc các bạn một ngày tốt lành.
Mấy bạn giúp mình giải thích bài hóa này với nha, mình biết không liên quan lắm, nhưng cũng rất mong các bạn giúp mình:Đề bài là Trong các CTHH sau , CTHH nào viết sai , sửa lại cho đúng:Và có một bài là ZnOH2 mà Zn(II), OH2(I) nên CTHH này sai, đúng hông? mấy bạn trong lớp tui ai cũng sửa lại là Zn(OH2)2 nhưng cô mình bảo sai, mình không hiểu cô giảng sao hết @_@, nên nhờ mấy bạn giải thích hộ mình với nha! Mình hổng có gì hết, nếu mấy bạn giúp được mình mình sẽ tick đúng cho và kết bạn nha! Mì...
Đọc tiếp
Mấy bạn giúp mình giải thích bài hóa này với nha, mình biết không liên quan lắm, nhưng cũng rất mong các bạn giúp mình:
Đề bài là Trong các CTHH sau , CTHH nào viết sai , sửa lại cho đúng:
Và có một bài là ZnOH2 mà Zn(II), OH2(I) nên CTHH này sai, đúng hông? mấy bạn trong lớp tui ai cũng sửa lại là Zn(OH2)2 nhưng cô mình bảo sai, mình không hiểu cô giảng sao hết @_@, nên nhờ mấy bạn giải thích hộ mình với nha! Mình hổng có gì hết, nếu mấy bạn giúp được mình mình sẽ tick đúng cho và kết bạn nha! Mình cảm ơn trước! Mong các bạn giúp đỡ cho!
(oh) hóa trị 1 mà zn hóa trị 2=> cthh la zn(oh)2
với lại ko có oh2 dau chi co OH hoac la H2O
Đúng 0
Bình luận (0)
phải viết là Zn(OH)2 vì nhóm (OH) hóa trị I
Đúng 0
Bình luận (0)
Nhưng mà Zn có hóa trị là II, nhóm (OH2) có hóa trị là I, nếu như vậy, theo CTHH, ta có:
\(x.II=y.I\Rightarrow\frac{X}{Y}=\frac{I}{II}\Rightarrow X=1;Y=2.\)
Vậy CTHH của hợp chất là: Zn(OH2)2 chứ nguyên nhóm (OH2 ) có hóa trị là I mà chứ đâu phải nhóm (OH). Xem lại giùm mình đi bạn!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mình vẽ hình và giải bài được không ạ? Mai mình ktra e nhưng đọc bài vẫn ko vẽ được hình nên mình cần lấy bài này làm mẫu cho mấy bài tiếp theo. Mình cảm ơn ạ💜💜💜
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành
Đúng 0
Bình luận (0)
É ô ét ai giúp mình bài này với ạ, sẵn tiện giải thích cho mình với được ko ạ hiện giờ mình đang cần gấp lắm ạ mai mình thi rồi nên mong cao nhân nào giải bài với giải thích bài này cho mình với ạ
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}\) \(\dfrac{2^{11}.9^3}{3^5.16^2}\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
Đúng 2
Bình luận (0)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
Đúng 2
Bình luận (0)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
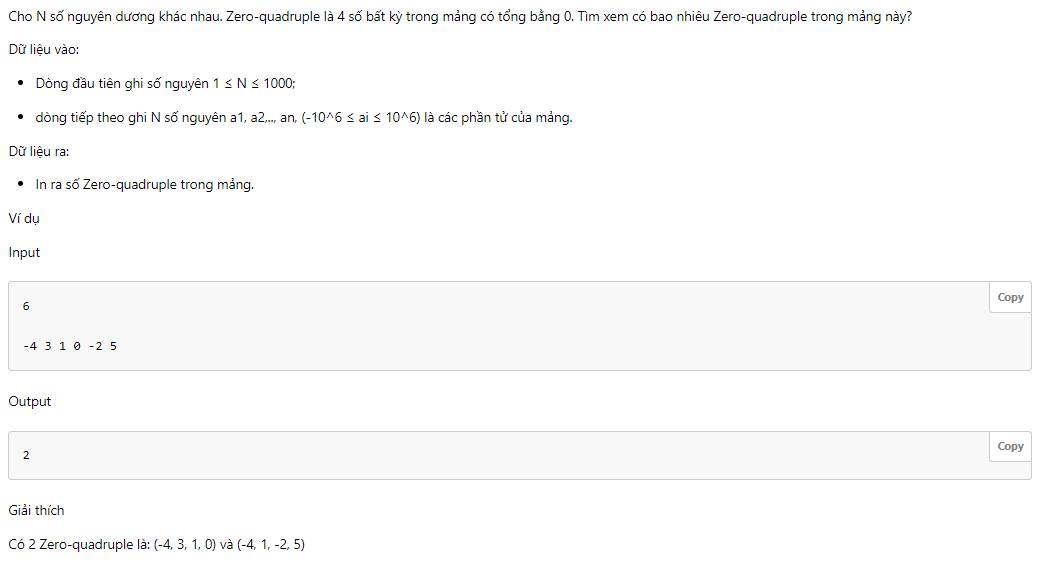 Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
cho biết một ngươi không biết sống tự lập thì họ sẽ như thế nào( cho vd)giúp mình vs! làm kĩ cái vd giúp mình nha pleas pleasvì ko có bài 4 sống tự lập nên mình để đại=))

hãy giúp mình bài 9c, 10, 11, 12, 13. Mọi người làm đc bài nào thì giúp mình bài ý không cần làm hết cả 4 đâu ạ 1 bài thôi cũng đc mà cả 4 thì càng tốt ạ cảm ơn mọi người
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
Đúng 0
Bình luận (0)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
Đúng 0
Bình luận (0)
13 b) \(\left(a+b\right)\left(ab+1\right)\ge2\sqrt{ab}.2\sqrt{ab}=4ab\)
Dấu = xảy ra khi a=b=1
Đúng 0
Bình luận (0)





