2^2016x2^x-1=2^2015
TC
Những câu hỏi liên quan
cho phương trình x^2-2(m+1)x+m-3=0 có hai nghiệm x1, x2.
chứng minh rằng biểu thức Q=x1(2017-2016x2)+x2(2017-2018x1) không phụ thuộc vào giá trị của m
\(Q=2017x_1-2016x_1x_2+2017x_2-2018x_1x_2\)
\(=2017\left(x_1+x_2\right)-4034x_1x_2\)
\(=2017\left(2m+2\right)-4034\left(m-3\right)\)
=4034m+4034-4034m+12102
=16136
Đúng 0
Bình luận (0)
K - 2016 = 1 + ( 1+ 2) + (1+2+3)+...+(1+2+3+...+2017) /2017x1+2016x2+2015x3+...+2x2016+1x2017
k=
H24
27 tháng 11 2023 lúc 21:16
Tìm giá trị nhỏ nhất của biểu thức B= x4+2016x2+4028 / x2+2
\(B=\dfrac{x^4+2016x^2+4028}{x^2+2}\)
\(=\dfrac{x^4+2x^2+2014x^2+4028}{x^2+2}\)
\(=x^2+2014>=2014\forall x\)
Dấu '=' xảy ra khi x=0
Đúng 0
Bình luận (0)
Tính K-2016 \(=\frac{1+\left(1+2\right)+\left(1+2+3\right)+.......+\left(1+2+3+.......2017\right)}{2017x1+2016x2+2015x3+.......+2x2016+1x2017}\)
xét tử số: tử số gồm có 2017 số hạng
số 1 xuất hiện 2017 lần
số 2 xuất hiện 2016 lần
số 3 xuất hiện 2015 lần
...
số 2017 xuất hiện 1 lần
=> =1.2017+2.2016+3.2015+...+2017.1
từ đó => kq = 1
Đúng 0
Bình luận (0)
Cho phương trình
2016
x
2
-
1
+
x
2
-
1
.
2017
x
1
1
Khẳng định nào dưới đây đúng? A. Phương trình (1) có nghiệm duy nhất. B. Phương trình (1) vô nghiệm. C. Phương trì...
Đọc tiếp
Cho phương trình 2016 x 2 - 1 + x 2 - 1 . 2017 x = 1 1 Khẳng định nào dưới đây đúng?
A. Phương trình (1) có nghiệm duy nhất.
B. Phương trình (1) vô nghiệm.
C. Phương trình (1) có tổng các nghiệm bằng 0.
D. Phương trình (1) có nhiều hơn hai nghiệm.
Chọn C.
=>Phương trình đã cho có 2 nghiệm và tổng hai nghiệm là 0
Đúng 0
Bình luận (0)
Cho phương trình
2016
x
2
-
1
+
x
2
-
1
.
2017
x
1
(1). Khẳng định nào dưới đây đúng? A. Phương trình (1) có nghiệm duy nhất B. Phương trình (1) có hai nghiệm phân biệt C. Phương trình (1) có tổng...
Đọc tiếp
Cho phương trình 2016 x 2 - 1 + x 2 - 1 . 2017 x = 1 (1). Khẳng định nào dưới đây đúng?
A. Phương trình (1) có nghiệm duy nhất
B. Phương trình (1) có hai nghiệm phân biệt
C. Phương trình (1) có tổng các nghiệm bằng 0
D. Phương trình (1) có nhiều hơn hai nghiệm
Chọn D.
Nhẩm pt có 2 nghiệm x = ±1 suy ra loại A
Nếu B đúng thì C đúng suy ra loại B suy ra pt có nhiều hơn 2 nghiệm chọn D.
Đúng 0
Bình luận (0)
Cho phương trình
2016
x
2
-
1
+
x
2
-
1
.
2017
x
1
. Mệnh đề nào sau đây là đúng? A. Phương trình đã cho có tổng các nghiệm bằng 0. B. Phương trình đã cho có nghiệm duy nhất. C. Phương trình đã cho...
Đọc tiếp
Cho phương trình 2016 x 2 - 1 + x 2 - 1 . 2017 x = 1 . Mệnh đề nào sau đây là đúng?
A. Phương trình đã cho có tổng các nghiệm bằng 0.
B. Phương trình đã cho có nghiệm duy nhất.
C. Phương trình đã cho có hai nghiệm dương phân biệt.
D. Phương trình đã cho có nhiều hơn hai nghiệm.
Chọn A.
+Nếu 
thì x2 – 1 > 0. Suy ra 
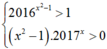
. Do đó phương trình đã cho vô nghiệm.
+ Nếu -1 < x < 1 thì x2 - 1 < 0. Suy ra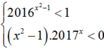 
. Do đó phương trình đã cho vô nghiệm.
+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.
Suy ra phương trình đã cho có tổng các nghiệm bằng 0.
Đúng 0
Bình luận (0)
Trong các hàm số
y
x
+
2
−
x
−
2
,
y
2
x
+
1
+
4
x
2
−
4
x
+
1
,...
Đọc tiếp
Trong các hàm số y = x + 2 − x − 2 , y = 2 x + 1 + 4 x 2 − 4 x + 1 , y = x ( x − 2 ) , y = x + 2015 + x − 2015 x + 2015 − x − 2015 có bao nhiêu hàm số lẻ?
A. 1
B. 2
C. 3
D. 4
\(x+2015\frac{1}{2}=\sqrt{1+2015^2+\frac{2015^2}{20162}}+\frac{2015}{2016}\)