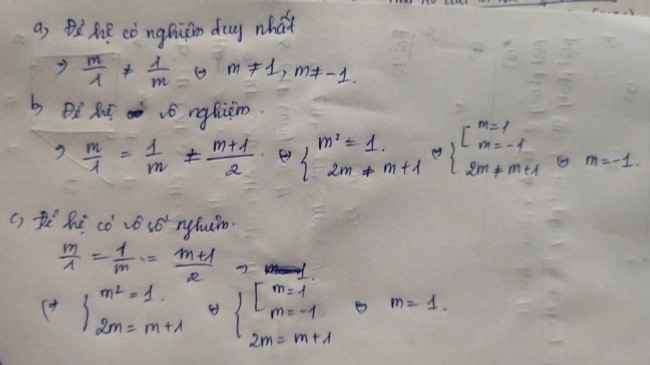Tìm a để phương trình |x-4|-x=2a có vô số nghiệm
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
DN
Những câu hỏi liên quan
Tìm m để hệ phương trình mx+ y = m + 1 và x+ my = 2
a)Có 1 nghiệm duy nhất
b)Vô nghiệm
c)Vô số nghiệm
Cho phương trình m(x-4)-2x=4(1-m) (với m là tham số)
a) Giải phương trình với m=0, m=-1, m=-3
b)Tìm m để phương trình vô nghiệm
c)Tìm m để phương trình có vô số nghiệm
d)Tìm m để phương trình có nghiệm dương duy nhất
e)Tìm m để phương trình có nghiệm duy nhât nhỏ hơn 1
Tìm a để phương trình a^2 (x-3)=2(2a-1)-5a +x vô nghiệm
\(\Leftrightarrow a^2x-3a^2-4a+2+5a-x=0\)
\(\Leftrightarrow x\left(a^2-1\right)-3a^2+a+2=0\)
\(\Leftrightarrow x\left(a-1\right)\left(a+1\right)=\left(a-1\right)\left(3a+2\right)\)
Để pt vô nghiệm thì a+1=0
hay a=-1
Đúng 0
Bình luận (0)
Cho hệ phương trình
\(\left\{{}\begin{matrix}x+my=4\\nx+y=-3\end{matrix}\right.\)
a/ Tìm m, n để hệ phương trình có nghiệm : (x;y) = (-2 ;3)
b/ Tìm m , n để hệ phương trình có vô số nghiệm
a Để hpt có nghiệm \(\left(x;y\right)=\left(-2;3\right)\) \(\Rightarrow\left\{{}\begin{matrix}-2+3m=4\\-2n+3=-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3m=6\\-2n=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\n=2\end{matrix}\right.\)
b Để hpt có vô số nghiệm \(\Leftrightarrow\dfrac{1}{n}=\dfrac{m}{1}=\dfrac{4}{-3}\) \(\left(\dfrac{a}{a'}=\dfrac{b}{b'}=\dfrac{c}{c'}\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{n}=-\dfrac{4}{3}\\m=-\dfrac{4}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{4}{3}\\n=-\dfrac{3}{4}\end{matrix}\right.\)
Vậy...
Đúng 0
Bình luận (0)
Bài 4:
a) Tìm m để phương trình sau có nghiệm duy nhất: 2x - mx + 2m - 1 = 0.
b) Tìm m để phương trình sau có vô số nghiệm: mx + 4 = 2x + m2.
c) Tìm m để phương trình sau có nghiệm duy nhất dương: (m2 - 4)x + m - 2 = 0
à bài này a nhớ (hay mất điểm ở bài này) ;v
Đúng 2
Bình luận (2)
xinloi cậu tớ muốn giúp lắm mà tớ ngu toán:)
Đúng 0
Bình luận (7)
a)Ta có \(2x-mx+2m-1=0\\ =>x\left(2-m\right)+2m-1=0\)
Để pt có nghiệm duy nhất thì \(a\ne0=>2-m\ne0\\=>m\ne2\)
b)Ta có \(mx+4=2x+m^2\\ =>mx+4-2x+m^2=0\\ =>\left(m-2\right)x=m^2-4\)
Để pt vô số nghiệm thì \(\left\{{}\begin{matrix}m-2=0\\m^2-4=0\end{matrix}\right.=>\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(=>m=2\)
c)Để pt có nghiệm duy nhất thì \(m^2-4\ne0>m\ne\pm2\)
Chắc vậy :v
Đúng 2
Bình luận (0)
Cho hệ phương trình x 2y=5 (1)
mx y=4 (2)
a) Tìm m để hệ phương trình vô nghiệm
b) Tìm m để hệ có nghiệp duy nhất
c) Tìm m để hệ vô số nghiệm
Cho phương trình: (m^2-7m+6)x+m^2-1=0 (với m là tham số)
a)tìm m để phương trình có nghiệm duy nhất.
b)tìm m để phương trình có vô số nghiệm.
c)tìm m để phương trình vô nghiệm.
Tìm a để phương trình 2(a-1)x - a(x-1) = 2a+3 vô nghiệm. kết quả là a =
cho phương trình mx^2 + 12 x − 4 = 0
a,giải phương trình với m=1
b,tìm m để phương trình có 2 nghiệm phân biệt
c,tìm m để phương trình có 2 nghiệm kép tìm nghiệm kép đó
d,tìm m để phương trình vô nghiệm
a) Thay \(m=1\) vào phương trình, ta được:
\(x^2+12x-4=0\) \(\Rightarrow\left[{}\begin{matrix}x=-6+2\sqrt{10}\\x=-6-2\sqrt{10}\end{matrix}\right.\)
Vậy ...
b)
+) Với \(m=0\) \(\Rightarrow12x-4=0\) \(\Leftrightarrow x=\dfrac{1}{3}\)
+) Với \(m\ne0\), ta có: \(\Delta'=36+4m\)
Để phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\) \(\Leftrightarrow m>-9\)
Vậy \(\left\{{}\begin{matrix}m\ne0\\m>-9\end{matrix}\right.\) thì phương trình có 2 nghiệm phân biệt
c) Để phương trình có nghiệm kép \(\Leftrightarrow\Delta'=0\) \(\Leftrightarrow m=-9\)
\(\Rightarrow-9x^2+12x-4=0\) \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(m=-9\) thì phương trình có nghiệm kép \(x_1=x_2=\dfrac{2}{3}\)
d) Để phương trình vô nghiệm \(\Leftrightarrow\Delta'< 0\) \(\Leftrightarrow m< -9\)
Vậy \(m< -9\) thì phương trình vô nghiệm
Đúng 0
Bình luận (0)