Nêu các trường hợp bằng nhau của tam giác, tam giác vuông.
TV
Những câu hỏi liên quan
Hãy nêu các trường hợp bằng nhau của tam giác vuông được suy ra từ các trường hợp bằng nhau của tam giác?
Gv đưa ra các hình vẽ,yêu cầu hs bổ sung các điều kiện về các cạnh hay về góc về được các tam giác vuông bằng nhau theo từng trường hợp đã học
Hai hs lên bảng ktra
Hs1 phát biểu các trường hợp bằng nhau của hai tam giác vuông đã học
Hs2 lên bảng làm bài(hình đã vẽ sẵn trên bảng phụ)
Đọc tiếp
Hãy nêu các trường hợp bằng nhau của tam giác vuông được suy ra từ các trường hợp bằng nhau của tam giác?
Gv đưa ra các hình vẽ,yêu cầu hs bổ sung các điều kiện về các cạnh hay về góc về được các tam giác vuông bằng nhau theo từng trường hợp đã học
Hai hs lên bảng ktra
Hs1 phát biểu các trường hợp bằng nhau của hai tam giác vuông đã học
Hs2 lên bảng làm bài(hình đã vẽ sẵn trên bảng phụ)
Các trường hợp bằng nhau của tam giác vuông:
-Hai cạnh góc vuông
-Cạnh góc vuông-góc nhọn kề
-Cạnh huyền-góc nhọn
-Cạnh huyền-cạnh góc vuông
Đúng 1
Bình luận (0)
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
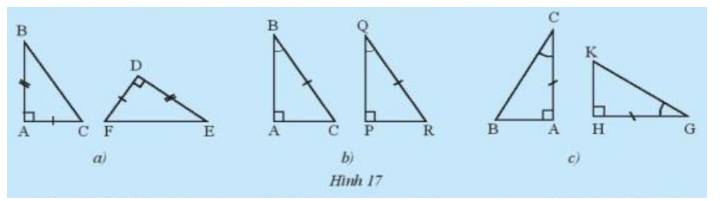
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) (c-g-c)
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) (g-c-g)
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) (g-c-g)
Đúng 0
Bình luận (0)
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
Đọc tiếp
1. hai tam giác bằng nhau là hai tam giác như thế nào?
2.có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
3.nêu các trường hợp bằng nhau của hai tam giác vuông.
4.phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là tam giác cân.
5.phát biểu định nghĩa và tính chất tam giác đều.Nêu các cách chưng minh một tam giác là tam giác đều.
6.phát biểu định lí Py-ta-go thuận và đảo.
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
Đúng 0
Bình luận (0)
- Nêu các trường hợp bằng nhau của hai tam giác.- Nêu các trường hợp bằng nhau của hai tam giác vuông.- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?Thế nào là tam giác đều? Nêu các tính chất
Đọc tiếp
- Nêu các trường hợp bằng nhau của hai tam giác.
- Nêu các trường hợp bằng nhau của hai tam giác vuông.
- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân
- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?
Thế nào là tam giác đều? Nêu các tính chất
hãy nêu tất cả các trường hợp bằng nhau của tam giác kể cả tam giác vuông.
Có 4 Trường hợp bằng nhau của tam giác :
Trường hợp bằng nhau thứ nhất của tam giác là : Cạnh cạnh cạnh
Trường hợp bằng nhau thứ hai của tam giác là : Cạnh Góc Cạnh
Trường hợp bằng nhau thứ ba của tam giác là : Góc Cạnh Góc
Trường hợp bằng nhau thứ tư của tam giác là : Cạnh Huyền Góc Nhọn
Nếu đúng thì cho mình tích nha bạn !
Đúng 0
Bình luận (0)
Có 3 trường hợp bằng nhau của tam giác, từ 3 điều trên suy ra thêm 4 trường hợp bằng nhau của tam giác vuông:
Cạnh Cạnh Cạnh => Cạnh Huyền Cạnh Góc Vuông
Cạnh Góc Cạnh => Hai Cạnh Góc Vuông
Góc Cạnh Góc => 1/Cạnh Huyền Góc Nhọn
2/Cạnh góc vuông và góc nhọn kề nó
Đúng 0
Bình luận (0)
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông? Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ....
Đọc tiếp
Nêu các trường hợp bằng nhau của hai tam giác, hai tam giác vuông?
Vẽ hình, ghi giảthuyết, kết luận cho từng trường hợp?
2. Nêu định nghĩa, tính chất của tam giác cân, tam giác đều?
3. Nêu định lý Pytago thuận và đảo, vẽ hình, ghi giả thuyết, kết luận của cả hai định lý
4. Nêu định lý về quan hệ giữa góc và cạnh đối diện trong tam giác, vẽ hình, ghi giả thiết, kết luận.
5. Nêu quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu, vẽ hình, ghigiả thuyết, kết luận cho từng mối quan hệ.
6. Nêu định lý về bất đẳng thức trong tam giác, vẽ hình, ghi giả thiết, kết luận
Câu 10: Phát biểu tiên đề Euclid.Câu 11: Nêu định lí tổng các góc trong tam giác.Câu 12: Nêu các trường hợp bằng nhau của tam giác thường, tam giác vuông?Câu 13: Nêu một số cách chứng minh đoạn thẳng bằng nhau, góc bằng nhau, đường thẳng vuông góc, tam giác cân, tam giác đều, 3 điểm thẳng hàng.Câu 14: nêu các đường đồng qui trong tam giác và tính chất của chúng?Câu 15: Nêu các công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình hộp chữ nhật, hình lập phương, hình l...
Đọc tiếp
Câu 10: Phát biểu tiên đề Euclid.
Câu 11: Nêu định lí tổng các góc trong tam giác.
Câu 12: Nêu các trường hợp bằng nhau của tam giác thường, tam giác vuông?
Câu 13: Nêu một số cách chứng minh đoạn thẳng bằng nhau, góc bằng nhau, đường thẳng vuông góc, tam giác cân, tam giác đều, 3 điểm thẳng hàng.
Câu 14: nêu các đường đồng qui trong tam giác và tính chất của chúng?
Câu 15: Nêu các công thức tính diện tích xung quanh, diện tích toàn phần, thể tích của hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
`@` `\text {Ans}`
`\downarrow`
`10,`
`@` Tiên đề Euclid được phát biểu như sau:
`-` Qua một điểm nằm ngoài 1 đường thẳng, chỉ có duy nhất `1` đường thẳng song song với đường thẳng đó.
`11,`
Định lý tổng `3` góc trong `1` `\triangle`
`-` Trong `1` `\triangle`, tổng số đo của `3` góc là `180^0`
`12,`
Các TH bằng nhau của `\triangle` thường:
`+` Cạnh - Cạnh - Cạnh
`+` Cạnh - Góc - Cạnh
`+` Góc - Cạnh - Góc
Các TH bằng nhau của `\triangle` vuông:
`+` Cạnh - Góc - Cạnh
`+` Góc - Cạnh - Góc
`+` Cạnh huyền - Góc vuông
`+` Cạnh góc vuông - Góc nhọn
`+` Cạnh huyền - Cạnh góc vuông
`+` Hai cạnh góc vuông
Đúng 5
Bình luận (0)
15:
Hình hộp chữ nhật
Sxq=(a+b)*2*h
Stp=Sxq+2*a*b
V=a*b*h
Hình lập phương
Sxq=a^2*4
Stp=a^2*6
V=a^3
Hình lăng trụ đứng tam giác
Sxq=C đáy*h
Stp=Sxq+2*S đáy
14:
Các đừog đồng quy là các đường cao, các đường trung tuyến, các đường phân giác, các đường trung trực
Các đường cao thì cắt nhau ở trực tâm của tam giác
Các đường trung tuyến thì cắt nhau ở trọng tâm của tam giác
Các đường phân giác thì cắt nhau ở tâm đừog tròn nội tiếp của tam giác
Các đường trung trực thì cắt nhau ở tâm đường tròn ngoại tiếp của tam giác
10:
Qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng đi qua nó và song song với đường thẳng đã cho
11:
Tổng ba góc trong một tam giác bằng 180 độ
Đúng 0
Bình luận (0)
`13,`
`@` 1 số cách c/m 2 đt' bằng nhau:
`+` Sử dụng tính chất của trung điểm
`+` Hai cạnh tương ứng trong `2` `\triangle` bằng nhau
`+` Hai cạnh bên của `\triangle` cân
`+` Sử dụng t/c của đường trung tuyến trong `\triangle` vuông (kì `2` lớp 7 mới)
`+` Tính chất của điểm nằm trên đường trung trực.
`@` 1 số cách c/m 2 góc bằng nhau:
`+` Hai góc tương ứng trong `2` `\triangle` `=` nhau
`+` Sử dụng t/c đường phân giác
`+` Sử dụng t/c của tiên đề Euclid (khi `2` đt' // thì các cặp góc sole trong bằng nhau, các cặp góc đồng vị bằng nhau)
`+` Hai góc đối đỉnh thì bằng nhau
`+`...
`@` 1 số cách c/m đường thẳng vuông góc:
`+` Chứng minh góc đó `= 90^0`
`+` T/c đường trực tâm của `\triangle` (kì 2 lớp 7)
`+` `2` đt' đó có chứa `2` tia phân giác của `2` góc kề bù
`+`...
`@` 1 số cách c/m tam giác cân:
`+` Chứng minh `2` cạnh bên bằng nhau
`+` Chứng minh `2` góc ở đáy bằng nhau
`+` T/c của các đường trong `\triangle` với `\triangle` cân
`@` 1 số cách c/m `3` điểm thẳng hàng:
`+` Chứng minh góc bẹt (tổng số đo của các góc trên đt' đó `= 180^0`)
`+` Chứng minh `3` điểm đó cùng thuộc `1` đt'
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
1 . Tìm các dấu hiệu để nhận bt 2 tam giác đồng dạng
2. So sánh các trường hợp đồng dạng của tam giác vs trường hợp bằng nhau của tam giác ( Nếu lên những điểm giống và khác nhau )
3. Nêu các dấu hiệu nhận bt tam giác vuông đồng dạng
1. Nêu các trường hợp bằng nhau của tam giác thường và tam giác vuông
( Viết bằng lời - Vẽ hình - Viết giả thiết , kết luận )
2. Nêu tính chất và góc của tam giác cân
Bài 1:
I. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh:
1) Vẽ tam giác biết độ dài 3 cạnh: (HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = 3cm, BC = 5cm, AC = 4cm.
2) Trường hợp bằng nhau cạnh – cạnh – cạnh:
“Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.”
II. Trường hợp bằng nhau thứ nhất của tam giác cạnh – góc – cạnh:
1) Vẽ tam giác biết độ dài 2 cạnh và 1 góc xen giữa:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = BC = 4cm,
2) Trường hợp bằng nhau cạnh – góc – cạnh:
“Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.”

Đúng 0
Bình luận (0)
* Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
* Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề ấy cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g-c-g)
* Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (ch-gn)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


