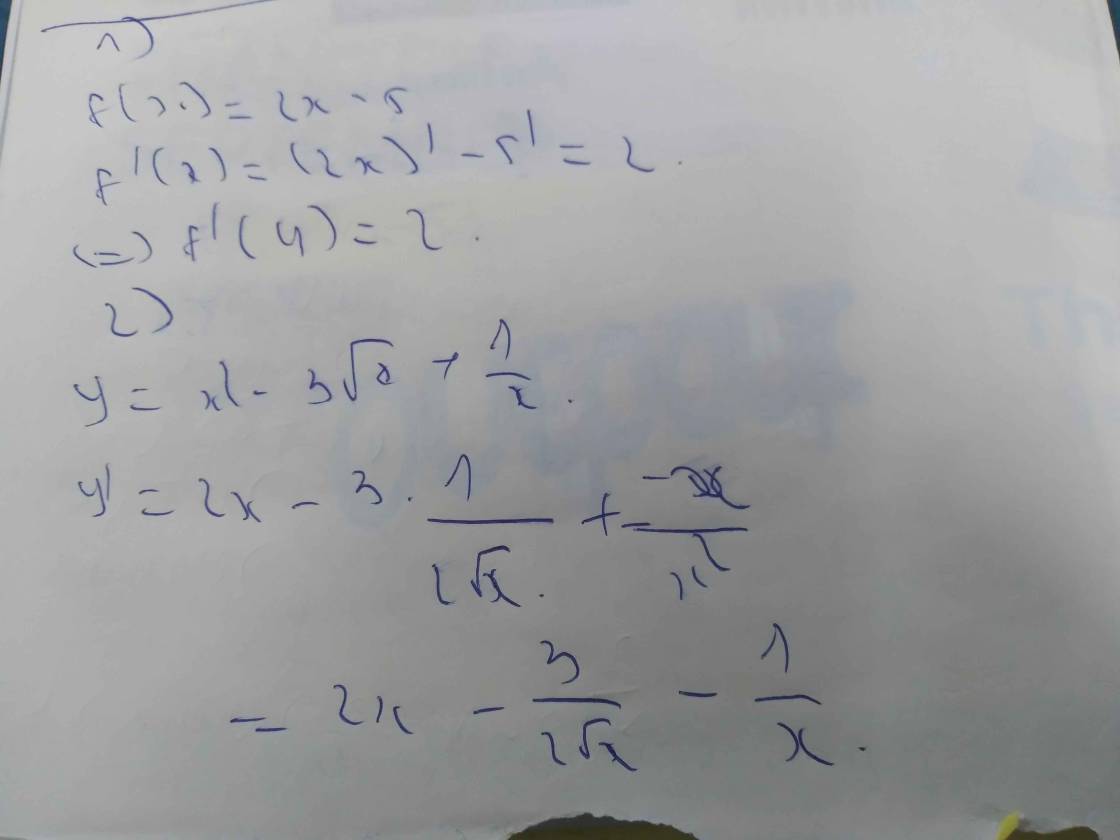Tìm GTNN của hàm số f(x)=x + 2 - 4\(\sqrt{x-1}\)
NC
Những câu hỏi liên quan
tìm gtln gtnn của hàm số
\(y=\sqrt{1+x}+\sqrt{1-x}+\dfrac{x^2}{4}\)
Lời giải:
TXĐ: $[-1;1]$
$y'=\frac{1}{2\sqrt{x+1}}-\frac{1}{2\sqrt{1-x}}+\frac{x}{2}$
$y'=0\Leftrightarrow x=0$
$f(0)=2$;
$f(1)=f(-1)=\sqrt{2}+\frac{1}{4}$
Vậy $f_{\min}=2; f_{\max}=\frac{1}{4}+\sqrt{2}$
Đúng 1
Bình luận (0)
a) Cho \(x\ge2\). GTNN của hàm số \(y=\dfrac{\sqrt{x-2}}{x}\)
b) GTNN của biểu thức \(f\left(x\right)=\dfrac{x}{\sqrt{x-1}}\) với x>1
a, \(y=\dfrac{\sqrt{x-2}}{x}=\sqrt{\dfrac{1}{x}-\dfrac{2}{x^2}}\ge0\)
\(min=0\Leftrightarrow\dfrac{1}{x}-\dfrac{2}{x^2}=0\Leftrightarrow x=2\)
b, Áp dụng BĐT Cosi:
\(f\left(x\right)=\dfrac{x}{\sqrt{x-1}}=\dfrac{x-1+1}{\sqrt{x-1}}=\sqrt{x-1}+\dfrac{1}{\sqrt{x-1}}\ge2\)
\(minf\left(x\right)=2\Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
Cho hàm số f(x)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tìm các g/trị của x để hàm số xác định
b) Tính f(\(4-2\sqrt{3}\)) và f(\(a^2\)) với a< -1
c) Tìm x sao cho f(x)=f(\(x^2\))
1. Tìm GTNN m của hàm số f(x)= \(\dfrac{4}{x}\) + \(\dfrac{x}{1-x}\) với 1>x>0
2. Tìm GTNN m của hàm số f(x)= \(\dfrac{1}{x}\) + \(\dfrac{1}{1-x}\) với 0<x<1
Giúp mk với nhé thanks trước.
1.
\(f\left(x\right)=\dfrac{4}{x}+\dfrac{x-1+1}{1-x}=\dfrac{2^2}{x}+\dfrac{1}{1-x}-1\ge\dfrac{\left(2+1\right)^2}{x+1-x}-1=8\)
\(f\left(x\right)_{min}=8\) khi \(x=\dfrac{2}{3}\)
2.
\(f\left(x\right)=\dfrac{1}{x}+\dfrac{1}{1-x}\ge\dfrac{4}{x+1-x}=4\)
\(f\left(x\right)_{min}=4\) khi \(x=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Tìm GTNN của hàm số y=\(\sqrt[3]{x^4+2x^2+1}\) - \(\sqrt[3]{x^2+1}+1\)
help me
Đặt \(\sqrt[3]{x^2+1}=t\left(t\ge1\right)\)
\(y=f\left(t\right)=t^2-t+1\)
\(minf\left(t\right)=f\left(1\right)=1\)
\(minf\left(t\right)=1\Leftrightarrow t=1\Leftrightarrow\sqrt[3]{x^2+1}=1\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)
Tìm gtnn của hàm số
\(f\left(x\right)=\sqrt{-x^2+4x+21}-\sqrt{-x^2+3x+10}\)
Tập xác định D của hàm số là \(\left[-2;5\right]\)
Ta có: \(f'\left(x\right)=\frac{-2x+4}{2\sqrt{-x^2+4x+21}}-\frac{-2x+3}{2\sqrt{-x^2+3x+10}}\)với \(x\in\left(-2;5\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left(-2x+4\right)\sqrt{-x^2+3x+10}=\)\(\left(-2x+3\right)\sqrt{-x^2+4x+21}\)
Suy ra \(\left(-2x+4\right)^2\left(-x^2+3x+10\right)=\)\(\left(-2x+3\right)^2\left(-x^2+4x+21\right)\)(1)
Khai triển ta được: \(51x^2-104x+29=0\)
\(\Delta=104^2-4.51.29=4900,\sqrt{\Delta}=70\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{104+70}{102}=\frac{29}{17}\\x=\frac{104-70}{102}=\frac{1}{3}\end{cases}}\)
Thử lại chỉ có \(\frac{1}{3}\)là nghiệm của (1)
Lập bảng biến thiên của hàm số f(x) suy ra \(f\left(x\right)_{min}=f\left(\frac{1}{3}\right)=\frac{\sqrt{200}-\sqrt{98}}{3}\)
@ Cool@ Không sai. Làm thế cũng đc nhưng mà lớp 9 đã học đạo hàm đâu?
Phải cuối năm lớp 11 mới học mà em,
Nguyễn Linh Chi Còn cách nào nữa không cô? Em tính dùng hệ số bất định rốt cuộc ra ngược dấu:(
Xem thêm câu trả lời
tìm GTNN của hàm số \(f\left(x\right)=\sqrt{x^2-2x+2}+\sqrt{x^2+2x+2}\)
\(=\sqrt{x^2-2x+1+1}+\sqrt{x^2+2x+1+1 }=\sqrt{\left(x-1\right)^2+1}+\sqrt{\left(x+1\right)^2+1}\)
Đúng 0
Bình luận (0)
Vì (x - 1)2 >= 0 và (x + 1)2 >= 0 nên Căn [(x - 1)2+1] + Căn [(x + 1)2+1] >= Căn [0 + 1] + Căn [0 + 1]
<=> Căn [(x - 1)2+1] + Căn [(x + 1)2+1] >= 2
Đúng 0
Bình luận (0)
Bạn Võ Thanh Quang xem lại bài giải vì Min f(x) = 2 . Lúc dấu "=" xảy ra ta không tìm được x
Do f(x) >=0
Ta có [f(x)]2 = x2 - 2x + 2 + x2 + 2x + 2 + 2\(\sqrt{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}\)
= 2x2 + 4 + 2\(\sqrt{x^4+4}\)\(\ge\)8
=> f(x) >= 2\(\sqrt{2}\)
=> Min f(x) = 2\(\sqrt{2}\) <=> x = 0
Đúng 0
Bình luận (0)
Tìm GTNN của hàm số
\(y=\sqrt{x+2\left(1+\sqrt{x+1}\right)}+\sqrt{x+2\left(1-\sqrt{x+1}\right)}\)
Ta có : \(\sqrt{x+1}\) có nghĩa khi `x >= -1` Từ đk ta có :
\(x+2\left(1+\sqrt{x+1}\right)=x+1+2\sqrt{x+1}+1=\left(\sqrt{x+1}+1\right)^2\)
\(\Leftrightarrow\sqrt{x+2\left(1+\sqrt{x+1}\right)}=\sqrt{x+1}+1\)
\(x+2\left(1-\sqrt{x+1}\right)=x+1-2\sqrt{x+1}+1=\left(\sqrt{x+1}-1\right)^2\\ \Leftrightarrow\sqrt{x+2\left(1-\sqrt{x+1}\right)}=\left|\sqrt{x+1}-1\right|\)
Ta có : \(y=\sqrt{x+1}+1+\left|\sqrt{x+1}-1\right|\) `(1)`
Ta bỏ dấu \(\left|\right|\) ở `1`
Ta có TH :
`-1<= x <= 0` ; lúc này \(\sqrt{x+1}-1\le0\)
nên : \(\left|\sqrt{x+1}-4\right|=1-\sqrt{x+1}\)
`1` trở thành : `y=2`
`x>0` lúc này \(\sqrt{x+1}-1>0\) nên
\(\left|\sqrt{x+1}-1\right|=\sqrt{x+1}-1\)
`1` trở thành : \(y=2\sqrt{x+1}>2\left(x>0\right)\)
Vì : \(y=\left\{{}\begin{matrix}2khi-1\le x\le0\\2\sqrt{x+1}kh\text{i}>0\end{matrix}\right.\)
gtnn của `y=2` với mọi \(x\in\left[-1;0\right]\)
Đúng 2
Bình luận (0)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Đúng 3
Bình luận (0)