Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.
Cho tam giác ABC có D là trung điểm của BC, trên tia đối của tia DA lấy điểm E sao cho DE=DA. Chứng minh
a/ DAB = DEC
b/ AC//BE
c/ Trên đoạn thẳng AB lấy điểm F, trên CE lấy điểm G sao cho AF=EG. Chứng minh F,D,G thẳng hàng
Hình vẽ, giả thiết, kết luận bạn vẽ và làm nha
\(a,\Delta DAB=\Delta DEC\)
\(\text{Xét }\Delta DAB=\Delta DEC\text{ có: }\)
\(DA=DE\left(gt\right)\left(1\right)\)
\(\widehat{ADB}=\widehat{EDC}\left(\text{đối đỉnh}\right)\left(2\right)\)
\(BD=CD\left(gt\right)\left(3\right)\)
\(\text{Từ (1), (2) và (3)}\Rightarrow\Delta DAB=\Delta DEC\left(c.g.c\right)\left(đpcm\right)\)
\(b,AC\text{//}BE\)
\(\text{Xét }\Delta ADC=\Delta EDB\text{ có: }\)
\(DA=DE\left(gt\right)\left(4\right)\)
\(\widehat{ADC}=\widehat{EDB}\left(\text{đối đỉnh}\right)\left(5\right)\)
\(CD=BD\left(gt\right)\left(6\right)\)
\(\text{Từ (4), (5) và (6)}\Rightarrow\Delta ADC=\Delta EDB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAC}=\widehat{DEB}\left(\text{2 góc tương ứng}\right)\)
\(\text{Mà 2 góc này ở vị trí so le trong của 2 đoạn thẳng AC và BE}\)
\(\Rightarrow AC\text{//}BE\left(đpcm\right)\)
\(c,F,D,G\text{ thẳng hàng}\)
\(\text{Ta có: }\Delta DAB=\Delta DEC\left(\text{câu a}\right)\)
\(\Rightarrow\widehat{BAD}=\widehat{CED}\left(\text{2 góc tương ứng}\right)\)
\(\text{Hay }\widehat{FAD}=\widehat{GED}\)
\(\text{Xét }\Delta ADF=\Delta EDG\text{ có: }\)
\(DA=DE\left(gt\right)\left(7\right)\)
\(\widehat{FAD}=\widehat{GED}\left(cmt\right)\left(8\right)\)
\(AF=EG\left(gt\right)\left(9\right)\)
\(\text{Từ (7), (8) và (9)}\Rightarrow\Delta ADF=\Delta EDG\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADF}=\widehat{EDG}\left(\text{2 góc tương ứng}\right)\)
\(\text{Lại có:}\widehat{EDG}+\widehat{ADG}=180^o\left(\text{kề bù}\right)\)
\(\text{Mà }\widehat{EDG}=\widehat{ADF}\left(cmt\right)\)
\(\Rightarrow\widehat{ADF}+\widehat{ADC}=180^o\left(10\right)\)
\(AD\text{ chung}\left(11\right)\)
\(\text{F và G khác phía đối với D}\left(12\right)\)
\(\text{Từ (10), (11) và (12)}\Rightarrow F,D,G\text{ thẳng hàng}\)
\(\text{Lưu ý: Bạn không thể chứng minh }\widehat{ADF}=\widehat{EDG}\text{ vì 2 góc đối đỉnh},\text{do nếu chứng}\)
\(\text{minh như vậy thì nghiễm nhiên bạn đã công nhân F,D,G thẳng hàng }\)
Cho tam giác ABC vuông tại A, kẻ đường phân giác BD (De AC) và kẻ DE vuông góc với BC (E thuộc BC). a) Chứng minh rằng: DA = DE b) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm E, D, F thẳng hàng?
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>E,D,F thẳng hàng
Cho tam giác ABC có D là trung điểm của BC, trên tia đối của tia DA lấy điểm E sao cho DE=DA. Chứng minh
a/ DAB = DEC
b/ AC//BE
c/ Trên đoạn thẳng AB lấy điểm F, trên CE lấy điểm G sao cho AF=EG. Chứng minh F,D,G thẳng hàng
xét tam giác ABC
ta có; DA=DE
DG=DC
góc ADB=gócEDC
suy ra tam giác DAB=DEC(C-G-C)
Cho tam giác ABC. Trên cạnh BC lấy điểm M. Trên tia đối của tia AB lấy D sao cho AB=AD. Trên tia đối của tia AC lấy E sao cho AC=AE. Trên tia đối của tia AM lấy F sao cho AM=AF. Chứng minh D, E, F thẳng hàng.
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
Cho tam giác ABC có M là trung điểm của BC. Trên tia đối tia DA lấy điểm E sao cho DE=DA. Chứng minh:
a, Tam giác DAB = tam giác DEC
b, AC//BE
c, Trên đường thẳng AB lấy điểm F, trên đường thẳng CE lấy điểm G sao cho: AF=EG. Chứng minh: 3 điểm F, D, G thẳng hàng.
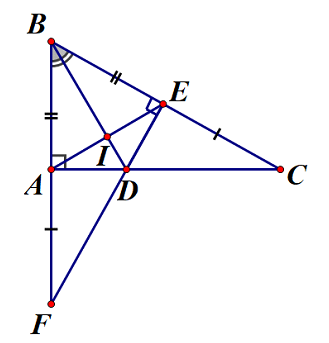
Bài 6 : Cho tam giác ABC có góc BAC = 90o, trên cạnh BC lấy điểm E sao cho BE=BA . Tia phân giác của góc ABC cắt AC ở D.
a. So sánh các độ dài DA và DE
b. Tính số đo góc BED
c. Trên tia đối của tia AB lấy điểm F sao cho AF=CE
Chứng minh ba điểm E,D,F thẳng hàng
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
AD=ED
AF=EC
Do đó: ΔADF=ΔEDC
Suy ra: \(\widehat{ADF}=\widehat{EDC}\)
=>\(\widehat{ADF}+\widehat{ADE}=180^0\)
=>E,F,D thẳng hàng
Bài 6 : Cho tam giác ABC có góc BAC = 90o, trên cạnh BC lấy điểm E sao cho BE=BA . Tia phân giác của góc ABC cắt AC ở D.
a. So sánh các độ dài DA và DE
b. Tính số đo góc BED
c. Trên tia đối của tia AB lấy điểm F sao cho AF=CE . Chứng minh ba điểm E,D,F thẳng hàng
a) Xét ΔADB và ΔEDB có:
BA = BE ( giả thiết )
Góc ABD = EBD ( BD là tia phân giác của góc ABE )
BD cạnh chung.
=> ΔADB = ΔEDB ( c.g.c )
=> DA = DE ( 2 cạnh tương ứng )
b) Vì ΔADB = ΔEDB nên góc DAB = DEB = 90 độ ( 2 góc tương ứng).
Mk vẽ hình ko đc đẹp cho lắm, thông cảm nha!
Cho tam giác ABC vuông tại A, phân giác DB , D thuộc AC. Qua D kẻ đường thẳng vuông góc với BC tại E. Trên tia đối của AB lấy điểm F sao cho AF=CE. Chứng minh 3 điểm E,D,F thẳng hàng