H24
Những câu hỏi liên quan
Cho hình thang cân ABCD có AB song song với CD và ab<cd
biết ad=bc
a) cm ab=bc
b) cm db là phân giác adc
Đề bài phải sửa thành "biết AD=AB" mới làm được
a/
ABCD là hình thàng cân => AD=BC
Mà AD=AB (gt)
=> AD=BC
b/
ABCD là hình thang cân
\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)
\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)
\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)
=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)
Ta có
Cung AB và cung BC có hai dây trương cung bằng nhau
AB=BC (cmt) => sđ cung AB = sđ cung BC (1)
\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)
\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB song song với CD) có AB = 7cm, BC = CD= 13cm. Kẻ các đường cao AK và BH
a) Chứng minh rằng CH=DK và AB = HK
b) Tính độ dài BH và diện tích hình thang ABCD
a: Xét ΔAKD vuông tại K và ΔBHC vuông tại H có
AD=BC
góc D=góc C
=>ΔAKD=ΔBHC
=>CH=DK
Xét tứ giác ABHK có
AB//HK
AK//HB
=>ABHK là hình bình hành
=>AB=HK
b: KH=AB=7cm
=>DK+HC=13-7=6cm
=>DK=HC=6/2=3cm
\(BH=\sqrt{13^2-3^2}=\sqrt{160}=4\sqrt{10}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}\cdot BH\cdot\left(AB+CD\right)\)
\(=\dfrac{1}{2}\cdot4\sqrt{10}\left(7+13\right)=40\sqrt{10}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB CD. Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a)i) Tam giác CEB là tam giác gì? Vì sao?ii) So sánh AD và BCb) Cho hình thang cân MNPQ có hai đáy là MN và PQ (Hình 6). So sánh MP và NQ
Đọc tiếp
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
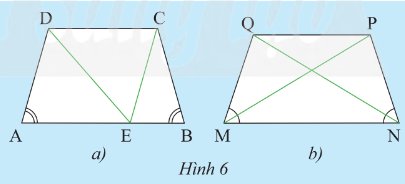
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho hình thang cân ABC, AB song song với CD, có AB= 13cm, CD=25cm, góc D = 45 độ.
S ABCD ?
Kẻ 2 đường cao AH và BK
=> ABKH là hình chữ nhật
=> AB = HK = 13cm
=> DH = KC = (DC - HK) : 2 = (25 - 13) : 2 = 6cm
Trong tam giác AHD có : góc ADH = 450; góc AHD = 900 => góc DAH = 450
=> tam giác AHD vuông cân tại H
=> AH = DH = 6cm
Vậy SABCD = \(\frac{\left(AB+CD\right).AH}{2}=\frac{\left(13+25\right).6}{2}=114cm^2\)
Đúng 0
Bình luận (0)
cho hình thang cân ABCD có đáy CD và AB ( AB<CD).Qua A kẻ đường thẳng song song với BC cắt đường chéo BD ở E qua B kẻ đường thẳng song song với AD cắt đường thẳng song song với AD cắt đường chéo AC tại F . a) CMR tứ giác DEFC là hình thang cân . b) tính độ dài EF biết AB=5cm , CD= 10cm
HELP ME ...............
Bài 1. Cho hình thang cân ABCD (AB//CD) có D̂ = 600, CD = 49 cm, AB = 15 cm. Qua B vẽ đường thẳng song song với AD cắt CD tại E
a) Chứng minh rằng BCE là tam giác đều.
b) Tính EC và chu vi hình thang ABCD.
Xét hình thang cân ABCD có
Góc D = 60 độ
=> Góc C=60 độ ( định lí hình thang cân)
Xét tamm giác BEC
Có góc C=60 độ
=> Tam giác BEC đều ( định lí tam giác đều)
Đúng 1
Bình luận (0)
Bài 1: Cho hình thang cân ABCD với cạnh đáy là AB và CD. Biết BD 6cm; BC 4cm. Hãy tính AC; AD. Bài 2: Tính diện tích của hình sau:Cho biết AB 2cm; CD BD 1cm; KD EG 3cm; HK 1cm, AB song song với CK; GE song song với CK.Bài 3: Cho hình thang cân MNPQ với hai đáy MN và PQ, PN 6cm; PM 10cm. Tính MQ, NQ Bài 4: Tính diện tích hình bên, biết AB 6cm, OB 3cm, OG 4cm, CD 12cm, ABCD là hình thang, BCEG là hình thoi, ba điểm A; B; E nằm trên một đường thẳng. Bài 5: Cho hình thang cân ABCD, ha...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD với cạnh đáy là AB và CD. Biết BD = 6cm; BC = 4cm. Hãy tính AC; AD.
Bài 2: Tính diện tích của hình sau:
Cho biết AB = 2cm; CD = BD = 1cm; KD = EG =3cm; HK = 1cm, AB song song với CK; GE song song với CK.
Bài 3: Cho hình thang cân MNPQ với hai đáy MN và PQ, PN = 6cm;
PM = 10cm. Tính MQ, NQ
Bài 4: Tính diện tích hình bên, biết AB = 6cm, OB = 3cm, OG = 4cm, CD = 12cm, ABCD là hình thang, BCEG là hình thoi, ba điểm A; B; E nằm trên một đường thẳng.
Bài 5: Cho hình thang cân ABCD, hai đáy AB và CD. Tính chu vi hình thang cân ABCD biết AB = 5cm; BC = 4cm; CD gấp đôi AB.
Làm giúp mình vs,ai làm nhanh mình cho một tick nhé
cho hình thang cân ABCD có AB song song với C (AB<CD) kể các đường cao AH ,BK ,chứng minh DH=CK
mấy cái câu kiểu này có hình thì hay bt mấy nhỉ
Đúng 0
Bình luận (0)
Xét tam giác ABC và tam giác BKC có :
góc AHD = góc AKC = 90 độ ( gt )
AD = BC ( gt )
góc D = góc C ( gt )
=> tam giác ABC = tam giác BKC ( ch - gn )
=> DH = CK
Đúng 3
Bình luận (0)
cho hình thang cân ABCD có AB song song với CD AB nhỏ hơn CD Biết ad = ab a Chứng minh AB = BC b Chứng minh DB là tia phân giác của ADC
`a)` Vì ABCD là hình thang cân
`=> AD = BC`
Có `AB = AD`
`=> BC = AB`
`b)`
Có `AB = AD`(GT)
`=>` tam giác `ABD ` cân
`=>` góc ADB = góc ABD 2
Vì `ABCD` là hình thang cân nên :
`AB//DC`
`=>` góc ABD = góc BDC 1
từ `(1); (2) =>` góc ADB = góc BDC
`=>` BD là pg cưa góc ADC
Đúng 2
Bình luận (0)
a: ABCD là hình thang cân
=>AD=BC
mà AD=AB
nên AB=BC
b: góc ABD=góc ADB
góc ABD=góc BDC
=>góc ADB=góc BDC
=>DB là phân giác của góc ADC
Đúng 0
Bình luận (0)






