Mọi người giúp em câu này làm sao ạ
TW
Những câu hỏi liên quan
mọi người giúp em làm câu này với ạ cảm ơn mọi người nhiêu ạ

C NHA BN CÂU 45 KO LÀM ĐC
Mọi người làm giúp em câu này ạ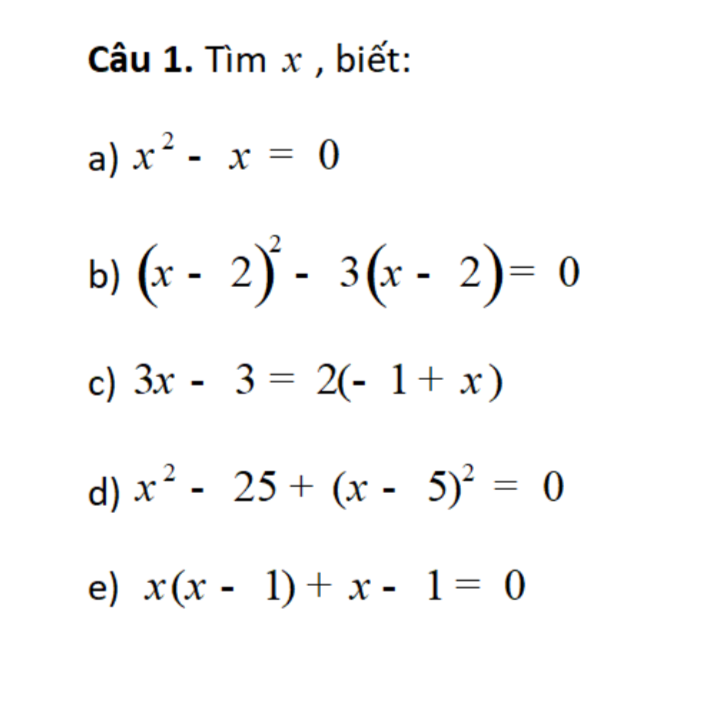
a) x^2 - x = 0
x(x-1)=0
x=0 hoặc x=1
b) (x-2)^2 - 3(x-2)=0
(x-2)(x-5)=0
x=2 hoặc x=5
c) pt <=> 3(x - 1) - 2(x - 1)=0
<=> x-1=0
<=> x = 1
Đúng 1
Bình luận (0)
a) \(\Rightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-2\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(\Rightarrow3\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow x-1=0\Rightarrow x=1\)
d) \(\Rightarrow\left(x-5\right)\left(x+5\right)+\left(x-5\right)^2=0\)
\(\Rightarrow\left(x-5\right).2x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
e) \(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d) pt <=> (x-5)(x+5) + (x-5)^2=0
<=> (x-5).2x=0
<=> x=0 hoặc x=5
e) pt <=> (x+1)(x-1)=0
<=> x=-1 hoặc x=1
Đúng 0
Bình luận (0)
mọi người giúp em làm 2 câu này với ạ em cảm ơn
Mọi người làm đầy đủ giúp em câu này với ạ :'( Em cảm ơn nhiều ạ!

\(n_{CO_2}=\dfrac{6,72}{22,4}=0,3mol\Rightarrow m_C=3,6g\)
\(n_{H_2O}=\dfrac{7,2}{18}=0,4mol\Rightarrow n_H=0,4\cdot2=0,8\Rightarrow m_H=0,8g\)
Nhận thấy: \(m_C+m_H=4,4=m_A\)
\(\Rightarrow A\) chỉ chứa hai nguyên tố C và H.
Gọi CTHH là \(C_xH_y\).
\(\Rightarrow x:y=n_C:n_H=0,3:0,8=3:8\)
\(\Rightarrow C_3H_8\)
Gọi CTĐGN là \(\left(C_3H_8\right)_n\)
Mà \(M=44\)g/mol\(\Rightarrow44n=44\Rightarrow n=1\)
Vậy CTPT là \(C_3H_8\)
A không làm mất màu dung dịch brom.
Đúng 2
Bình luận (0)
mọi người giúp em làm và giải thích câu này với ạ, em cám ơn nhiều ạ!

mọi người giúp em làm và giải thích câu này với ạ huhuu
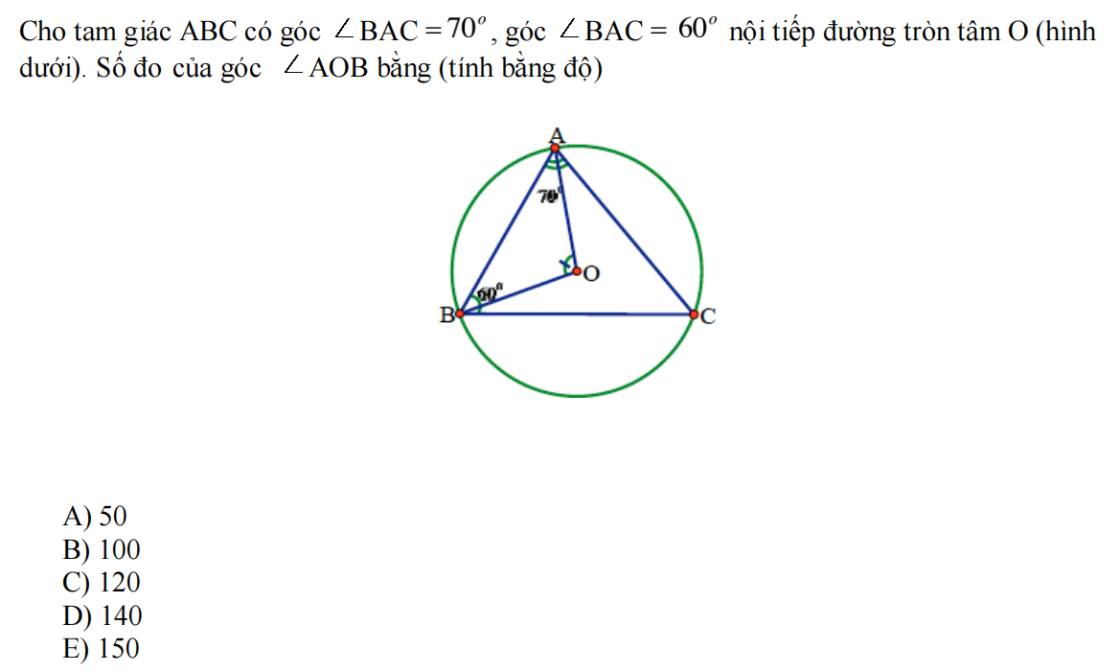
\(\widehat{ACB}=180^0-\left(\widehat{BAC}+\widehat{ABC}\right)=50^0\)
\(\Rightarrow\widehat{AOB}=2.\widehat{ACB}=100^0\) (góc ở tâm gấp đôi góc nội tiếp chắn cùng dây cung)
Đúng 1
Bình luận (1)
Mọi người giúp em mấy câu này với ạ!! Một vài câu cũng được mà làm hết thì càng tốt

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
Đúng 1
Bình luận (0)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
7.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-\left(x+1\right)+\left(x+1-\sqrt[3]{1+3x}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{1+2x}+x+1}+\dfrac{x^2\left(x+3\right)}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{1+2x}+x+1}+\dfrac{x+3}{\left(x+1\right)^2+\left(x+1\right)\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{3}{1+1+1}=1\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+3\right)=3\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi, giúp em mấy bài này với ạ. Hàng tá bài mà cô yêu cầu ngày mai nộp gấp quá, em không biết làm sao giờ. Cảm ơn mọi người ạ. 
8: Ta có: \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
Đúng 0
Bình luận (0)
Mọi người giúp em làm mấy bài này được không ạ,em sắp thi tới nơi rồi ạ,mọi người làm giúp em thì em cảm ơn ạ 😘😘😘😘





