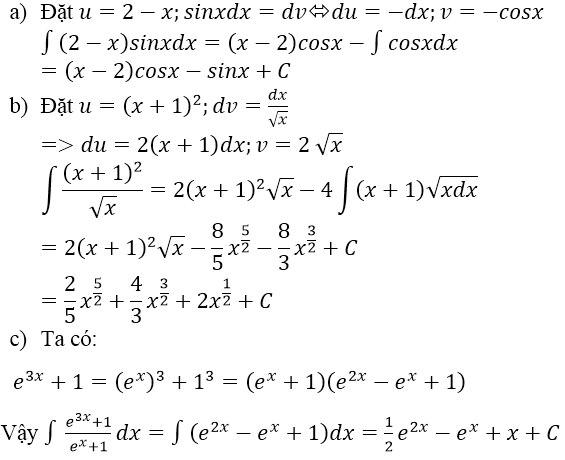Câu 2)

Đặt \(\left\{\begin{matrix} u=\ln ^2x\\ dv=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=2\frac{\ln x}{x}dx\\ v=\frac{x^3}{3}\end{matrix}\right.\Rightarrow I=\frac{x^3}{3}\ln ^2x-\frac{2}{3}\int x^2\ln xdx\)

Đặt \(\left\{\begin{matrix} k=\ln x\\ dt=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} dk=\frac{dx}{x}\\ t=\frac{x^3}{3}\end{matrix}\right.\Rightarrow \int x^2\ln xdx=\frac{x^3\ln x}{3}-\int \frac{x^2}{3}dx=\frac{x^3\ln x}{3}-\frac{x^3}{9}+c\)

Do đó \(I=\frac{x^3\ln^2x}{3}-\frac{2}{9}x^3\ln x+\frac{2}{27}x^3+c\)

Câu 3:

\(I=\int\frac{2}{\cos 2x-7}dx=-\int\frac{2}{2\sin^2x+6}dx=-\int\frac{dx}{\sin^2x+3}\)

Đặt \(t=\tan\frac{x}{2}\Rightarrow \left\{\begin{matrix} \sin x=\frac{2t}{t^2+1}\\ dx=\frac{2dt}{t^2+1}\end{matrix}\right.\)

\(\Rightarrow I=-\int \frac{2dt}{(t^2+1)\left ( \frac{4t^2}{(t^2+1)^2}+3 \right )}=-\int\frac{2(t^2+1)dt}{3t^4+10t^2+3}=-\int \frac{2d\left ( t-\frac{1}{t} \right )}{3\left ( t-\frac{1}{t} \right )^2+16}=\int\frac{2dk}{3k^2+16}\)

Đặt \(k=\frac{4}{\sqrt{3}}\tan v\). Đến đây dễ dàng suy ra \(I=\frac{-1}{2\sqrt{3}}v+c\)

Câu 6)

\(I=-\int \frac{\left ( 1-\frac{1}{x^2} \right )dx}{x^2+2+\frac{1}{x^2}}=-\int \frac{d\left ( x+\frac{1}{x} \right )}{\left ( x+\frac{1}{x} \right )^2}=-\frac{1}{x+\frac{1}{x}}+c=-\frac{x}{x^2+1}+c\)

Câu 8)

\(I=\int \ln \left(\frac{x+1}{x-1}\right)dx=\int \ln (x+1)dx-\int \ln (x-1)dx\)

\(\Leftrightarrow I=\int \ln (x+1)d(x+1)-\int \ln (x-1)d(x-1)\)

Xét \(\int \ln tdt\) ta có:

Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=dt\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=t\end{matrix}\right.\Rightarrow \int \ln tdt=t\ln t-\int dt=t\ln t-t+c\)

\(\Rightarrow I=(x+1)\ln (x+1)-(x+1)-(x-1)\ln (x-1)+x-1+c\)

\(\Leftrightarrow I=(x+1)\ln(x+1)-(x-1)\ln(x-1)+c\)

\(I=\dfrac{1}{2}\int f\left(x^2\right).d\left(x^2\right)=\dfrac{1}{2}x^2\sqrt{\left(x^2\right)^2+1}=\dfrac{1}{2}x^2\sqrt{x^4+1}\)

\(I=\dfrac{1}{2}\int f\left(x^2\right)d\left(x^2\right)=\dfrac{1}{2}x^2\sqrt{\left(x^2\right)^2+1}+C=\dfrac{1}{2}x^2\sqrt{x^4+1}+C\)

Làm tiếp

\(t=\sqrt{x^4+1}\Rightarrow dt=\dfrac{1}{2}.\left(x^4+1\right)^{-\dfrac{1}{2}}.4.x^3=\dfrac{2x^3}{\sqrt{x^4+1}}dx\Rightarrow dx=\dfrac{1}{2}.\dfrac{\sqrt{x^4+1}dt}{x^3}dt\)

\(\Rightarrow\int x.\dfrac{2x^4+1}{\sqrt{x^4+1}}dx=\dfrac{1}{2}\int x.\dfrac{2x^4+1}{\sqrt{x^4+1}}.\dfrac{\sqrt{x^4+1}}{x^3}dt=\dfrac{1}{2}\int\dfrac{2x^4+1}{x^2}dt=\dfrac{1}{2}\int2x^2dt+\dfrac{1}{2}\int\dfrac{dt}{x^2}=\int\sqrt{t^2-1}dt+\dfrac{1}{2}\int\dfrac{dt}{\sqrt{t^2-1}}\)

Tất cả đã về dạng cơ bản

Xet \(I_1=\int\sqrt{t^2-1}dt\)

\(\sqrt{t^2-1}=\dfrac{1}{2}.\dfrac{2t^2-1}{\sqrt{t^2-1}}-\dfrac{1}{2\sqrt{t^2-1}}=\dfrac{1}{2}\left(\sqrt{t^2-1}+\dfrac{t^2}{\sqrt{t^2-1}}\right)-\dfrac{1}{2\sqrt{t^2-1}}\)

\(\left(t\sqrt{t^2-1}\right)'=\sqrt{t^2-1}+\dfrac{t^2}{\sqrt{t^2-1}}\)

\(\Rightarrow\int\sqrt{t^2-1}dt=\dfrac{1}{2}\int\left(t\sqrt{t^2-1}\right)'dt-\dfrac{1}{2}\int\dfrac{dt}{\sqrt{t^2-1}}=\dfrac{1}{2}\left(t\sqrt{t^2-1}\right)-\dfrac{1}{2}ln\left|t+\sqrt{t^2-1}\right|+C\)

\(\Rightarrow I=\dfrac{1}{2}t\sqrt{t^2-1}-\dfrac{1}{2}ln\left|t+\sqrt{t^2-1}\right|+\dfrac{1}{2}ln\left|t+\sqrt{t^2-1}\right|=\dfrac{1}{2}t\sqrt{t^2-1}=\dfrac{1}{2}.x^2\sqrt{x^4+1}+C\)

Một cách làm khác đến từ vị trí của dân chuyên Toán :v Hãi hơn cái cách mình làm bao nhiêu ra. À bạn ấy làm từ cái tính nguyên hàm \(\int x.\dfrac{2x^4+1}{\sqrt{x^4+1}}dx\) trở đi nhá!

1/ \(I=\int\limits^1_0\dfrac{2x+1}{x^2+x+1}dx=\int\limits^1_0\dfrac{d\left(x^2+x+1\right)}{x^2+x+1}=ln\left|x^2+x+1\right||^1_0=ln3\)

2/ \(\int\limits^{\dfrac{1}{2}}_0\dfrac{5x}{\left(1-x^2\right)^3}dx=-\dfrac{5}{2}\int\limits^{\dfrac{1}{2}}_0\dfrac{d\left(1-x^2\right)}{\left(1-x^2\right)^3}=\dfrac{5}{4}\dfrac{1}{\left(1-x^2\right)^2}|^{\dfrac{1}{2}}_0=\dfrac{35}{36}\)

3/ \(\int\limits^1_0\dfrac{2x}{\left(x+1\right)^3}dx\Rightarrow\) đặt \(x+1=t\Rightarrow x=t-1\Rightarrow dx=dt;\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=1\Rightarrow t=2\end{matrix}\right.\)

\(I=\int\limits^2_1\dfrac{2\left(t-1\right)dt}{t^3}=\int\limits^2_1\left(\dfrac{2}{t^2}-\dfrac{2}{t^3}\right)dt=\left(\dfrac{-2}{t}+\dfrac{1}{t^2}\right)|^2_1=\dfrac{1}{4}\)

4/ \(\int\limits^1_0\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}dx\)

Kĩ thuật chung là tách và sử dụng hệ số bất định như sau:

\(\dfrac{4x-2}{\left(x^2+1\right)\left(x+2\right)}=\dfrac{ax+b}{x^2+1}+\dfrac{c}{x+2}=\dfrac{\left(a+c\right)x^2+\left(2a+b\right)x+2b+c}{\left(x^2+1\right)\left(x+2\right)}\)

\(\Rightarrow\left\{{}\begin{matrix}a+c=0\\2a+b=4\\2b+c=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=0\\a=-c=2\end{matrix}\right.\)

\(\Rightarrow I=\int\limits^1_0\left(\dfrac{2x}{x^2+1}-\dfrac{2}{x+2}\right)dx=\int\limits^1_0\dfrac{d\left(x^2+1\right)}{x^2+1}-2\int\limits^1_0\dfrac{d\left(x+2\right)}{x+2}=ln\dfrac{8}{9}\)

5/ \(\int\limits^1_0\dfrac{x^2dx}{x^6-9}\Rightarrow\) đặt \(x^3=t\Rightarrow3x^2dx=dt\Rightarrow x^2dx=\dfrac{1}{3}dt;\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=1\Rightarrow t=1\end{matrix}\right.\)

\(I=\dfrac{1}{3}\int\limits^1_0\dfrac{dt}{t^2-9}=\dfrac{1}{18}\int\limits^1_0\left(\dfrac{1}{t-3}-\dfrac{1}{t+3}\right)dt=\dfrac{1}{18}ln\left|\dfrac{t-3}{t+3}\right||^1_0=-\dfrac{1}{18}ln2\)

6/ Tương tự câu 4, sử dụng hệ số bất định ta tách được:

\(\int\limits^2_1\dfrac{2x-1}{x^2\left(x+1\right)}dx=\int\limits^2_1\left(\dfrac{3x-1}{x^2}-\dfrac{3}{x+1}\right)dx=\int\limits^2_1\left(\dfrac{3}{x}-\dfrac{1}{x^2}-\dfrac{3}{x+1}\right)dx\)

\(=\left(3ln\left|\dfrac{x}{x+1}\right|+\dfrac{1}{x}\right)|^2_1=3ln\dfrac{4}{3}-\dfrac{1}{2}\)

\(I=\int\dfrac{x}{1-cos2x}dx=\int\dfrac{x}{2sin^2x}dx\)

Đặt \(\left\{{}\begin{matrix}u=\dfrac{x}{2}\\dv=\dfrac{1}{sin^2x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{2}\\v=-cotx\end{matrix}\right.\)

\(\Rightarrow I=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int cotxdx=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{cosx.dx}{sinx}\)

\(=\dfrac{-x.cotx}{2}+\dfrac{1}{2}\int\dfrac{d\left(sinx\right)}{sinx}=\dfrac{-x.cotx}{2}+\dfrac{1}{2}ln\left|sinx\right|+C\)

2/ Câu 2 bữa trước làm rồi, bạn coi lại nhé

3/ \(I=\int\left(2x+1\right)ln^2xdx\)

Đặt \(\left\{{}\begin{matrix}u=ln^2x\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{2lnx}{x}dx\\v=x^2+x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x\right)ln^2x-\int\left(2x+2\right)lnxdx=\left(x^2+x\right)ln^2x-I_1\)

\(I_1=\int\left(2x+2\right)lnx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=lnx\\dv=\left(2x+2\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=x^2+2x\end{matrix}\right.\)

\(\Rightarrow I_1=\left(x^2+2x\right)lnx-\int\left(x+2\right)dx=\left(x^2+2x\right)ln-\dfrac{x^2}{2}+2x+C\)

\(\Rightarrow I=\left(x^2+x\right)ln^2x-\left(x^2+2x\right)lnx+\dfrac{x^2}{2}-2x+C\)

4/ \(I=\int\left(2x-1\right)cosx.dx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x-1\\dv=cosx.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=sinx\end{matrix}\right.\)

\(\Rightarrow I=\left(2x-1\right)sinx-2\int sinx.dx=\left(2x-1\right)sinx+2cosx+C\)

5/ \(I=\int\left(x^2+x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=x^2+x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\left(2x+1\right)dx\\v=e^x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x+1\right)e^x-\int\left(2x+1\right)e^xdx\)

\(I_1=\int\left(2x+1\right)e^xdx\) \(\Rightarrow\left\{{}\begin{matrix}u=2x+1\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=e^x\end{matrix}\right.\)

\(\Rightarrow I_1=\left(2x+1\right)e^x-2\int e^xdx=\left(2x+1\right)e^x-2e^x+C=\left(2x-1\right)e^x+C\)

\(\Rightarrow I=\left(x^2+x+1\right)e^x-\left(2x-1\right)e^x+C=\left(x^2-x+2\right)e^x+C\)

6/ \(I=\int\left(2x+1\right).ln\left(x+2\right)dx\)

\(\Rightarrow\left\{{}\begin{matrix}u=ln\left(x+2\right)\\dv=\left(2x+1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x+2}\\v=x^2+x\end{matrix}\right.\)

\(\Rightarrow I=\left(x^2+x\right)ln\left(x+2\right)-\int\dfrac{x^2+x}{x+2}dx\)

\(=\left(x^2+x\right)ln\left(x+2\right)-\int\left(x-1+\dfrac{2}{x+2}\right)dx\)

\(I=\left(x^2+x\right)ln\left(x+2\right)-\dfrac{x^2}{2}+x-2ln\left|x+2\right|+C\)

1) Đặt \(2+lnx=t\Leftrightarrow x=e^{t-2}\Rightarrow dx=e^{t-2}dt\)

\(I_1=\int\left(\frac{t-2}{t}\right)^2\cdot e^{t-2}\cdot dt=\int\left(1-\frac{4}{t}+\frac{4}{t^2}\right)e^{t-2}dt\\ =\int e^{t-2}dt-4\int\frac{e^{t-2}}{t}dt+4\int\frac{e^{t-2}}{t^2}dt\)

Có:

\(4\int\frac{e^{t-2}}{t^2}dt=-4\int e^{t-2}\cdot d\left(\frac{1}{t}\right)=-\frac{4\cdot e^{t-2}}{t}+4\int\frac{e^{t-2}}{t}dt\\ \Leftrightarrow4\int\frac{e^{t-2}}{t^2}dt-4\int\frac{e^{t-2}}{t^{ }}dt=-\frac{4\cdot e^{t-2}}{t}\)

Vậy \(I_1=\int e^{t-2}dt-\frac{4\cdot e^{t-2}}{t}=e^{t-2}-\frac{4e^{t-2}}{t}+C\)

3) Đặt \(t=\sqrt{1+\sqrt[3]{x^2}}\Rightarrow t^2-1=\sqrt[3]{x^2}\Leftrightarrow x^2=\left(t^2-1\right)^3\)

\(d\left(x^2\right)=d\left[\left(t^2-1\right)^3\right]\Leftrightarrow2x\cdot dx=6t\left(t^2-1\right)^2\cdot dt\)

\(I_3=\int\frac{3t\left(t^2-1\right)^2}{t}dt=3\int\left(t^4-2t^2+1\right)dt=...\)

5) Đặt \(\frac{2+x}{2-x}=4t^3\Leftrightarrow4t^3=\frac{4}{2-x}-1\)

\(d\left(4t^3\right)=d\left(\frac{4}{2-x}-1\right)\Leftrightarrow3t^2dt=\frac{1}{\left(2-x\right)^2}dx\)

\(I_5=\int\frac{3t^2}{t\sqrt[3]{4}}dt=\frac{3}{\sqrt[3]{4}}\int tdt=...\)

Biến đổi: ʃ\(\int\dfrac{1dx}{cosx\dfrac{\sqrt{2}}{2}\left(cosx-sinx\right)}=\int\dfrac{\sqrt{2}dx}{cos^2x\left(1-tanx\right)}=\int\dfrac{\sqrt{2}d\left(tanx\right)}{1-tanx}=-\sqrt{2}\ln trituyetdoi\left(1-tanx\right)\)

https://www.youtube.com/channel/UCzeAuHrGhk8hUszunoNtayw

Luyện Thi THPT Quốc Gia miễn phí 100%