cho a + b + c =1 .chứng minh 1/abc +9/a2+b2+c2 >54
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NT
Những câu hỏi liên quan
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Ngu kkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
cho (a+b+c)2=a2+b2+c2 và a,b,c ≠0. Chứng minh 1/a3+1/b3+1/c3=3/abc
\(\left(a+b+c\right)^2=a^2+b^2+c^2\)
=>\(a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
=>\(2\left(ab+bc+ac\right)=0\)
=>ab+bc+ac=0
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
=>\(\dfrac{\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3}{\left(abc\right)^3}=\dfrac{3}{abc}\)
=>\(\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3=3\left(abc\right)^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3\cdot ab\cdot bc\cdot\left(ab+bc\right)+\left(ac\right)^3=3\left(abc\right)^2\)
=>\(\left(-ac\right)^3-3\cdot ab\cdot bc\cdot\left(-ac\right)+\left(ac\right)^3-3\left(abc\right)^2=0\)
=>\(-a^3c^3+a^3c^3+3a^2b^2c^2-3a^2b^2c^2=0\)
=>0=0(đúng)
Đúng 1
Bình luận (0)
Cho các số thực dương a,b,c thỏa mãn a+b+c=3
Chứng minh rằng abc(1+a2)(1+b2)(1+c2)≤8
Cần gấp ko bạn
Nếu gấp thì sang web khác thử
Đúng 0
Bình luận (0)
cho a,b, thỏa mãn điều kiện a2 b2 c2 1 chứng minh abc 2 1 a b c ab bc ac ≥0
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
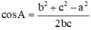
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Đúng 0
Bình luận (0)
a) Cho a, b, c thoả mãn a+b+c = abc
CMR: a(b2-1)( c2-1) + b(a2-1)( c2-1) + c(a2-1)( b2-1) = 4abc
86 vì ta học lớp 9
Ta có: \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)\)
\(=a\left(b^2c^2-b^2-c^2+1\right)+b\left(a^2c^2-a^2-c^2+1\right)\)
\(+c\left(a^2b^2-a^2-b^2+1\right)\)
\(=ab^2c^2-ab^2-ac^2+a+ba^2c^2-a^2b-bc^2+b\)
\(+ca^2b^2-a^2c-b^2c+c\)
\(=\left(ab^2c^2+ba^2c^2+ca^2b^2\right)+\left(a+b+c\right)\)
\(-\left(ab^2+ac^2+a^2b+bc^2+a^2c+b^2c\right)\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)\)\(-\left[ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left[ab\left(a+b+c\right)+bc\left(a+b+c\right)+ca\left(a+b+c\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(=abc\left(bc+ac+ab\right)+abc+3abc\)\(-abc\left(ab+bc+ca\right)=4abc\)
Vậy \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)=4abc\)(đpcm)
Chứng minh bất đẳng thức (a + 1)2 ≥ 4aChứng minh : (ac + bd)2 + (ad – bc)2 (a2 + b2)(c2 + d2) Cho a, b, c là các số dương. Chứng minh : a3 + b3 + abc ≥ ab(a + b + c)Mn giúp mik vs ;-;
Đọc tiếp
Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
Chứng minh : (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
Cho a, b, c là các số dương. Chứng minh : a3 + b3 + abc ≥ ab(a + b + c)
Mn giúp mik vs ;-;
a: \(\Leftrightarrow\left(a+1\right)^2-4a\ge0\)
hay \(\left(a-1\right)^2>=0\)(luôn đúng)
b: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)=VP\)
Đúng 1
Bình luận (1)
Cho a+b+c=0 ; \(\dfrac{1}{a}\)+\(\dfrac{1}{b}\)+\(\dfrac{1}{c}\)=0. Chứng minh rằng: a2+b2+c2=1
1/a+1/b+1/c=0
=>(ab+ac+bc)/abc=0
=> ab+ac+bc=0
(a+b+c)^2=a^2+b^2+c^2+2(ab+ac+bc)=0
=> a^2+b^2+c^2=0
Bạn xem lại đề nhé.
Đúng 1
Bình luận (0)
Bài 1. Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh rằng a = b =c.
\(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
Đúng 3
Bình luận (0)
Ta có: \(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow a=b=c\)
Đúng 0
Bình luận (0)
a2+b2+c2=ab+bc+caa2+b2+c2=ab+bc+ca
⇔2a2+2b2+2c2=2ab+2bc+2ca⇔2a2+2b2+2c2=2ab+2bc+2ca
⇔(a2−2ab+b2)+(b2−2bc+c2)+(c2−2ca+a2)=0⇔(a2−2ab+b2)+(b2−2bc+c2)+(c2−2ca+a2)=0
⇔(a−b)2+(b−c)2+(c−a)2=0⇔(a−b)2+(b−c)2+(c−a)2=0
⇔⎧⎪⎨⎪⎩a−b=0b−c=0c−a=0⇔{a−b=0b−c=0c−a=0 ⇔a=b=c
Đúng 0
Bình luận (0)



