cho đường tròn (O,R) từ điểm M nằm ngoài đường tròn kẻ tiếp tuyến MB,MC ; kẻ đường kính BD.chứng mibh BD//OM
NT
Những câu hỏi liên quan
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm...
Đọc tiếp
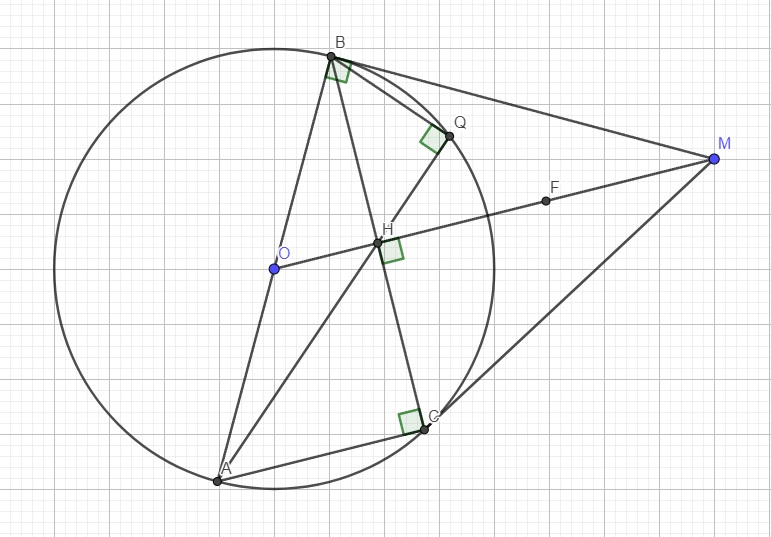
Cho đường tròn (O;R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B,C là tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA. a) Cm các điểm M,B,O,C cùng nằm trên 1 đg tròn b) Cm: CH^2=OH.HM c) Gọi F là trung điểm của MH,AH cắt (O) tại giao điểm thứ hai là Q.Cm tam giác MBH đồng dạng tam giác BAC và B,Q,F thẳng hàng
a. Câu này đơn giản em tự giải.
b.
Ta có: \(\left\{{}\begin{matrix}OB=OC=R\\MB=MC\left(\text{t/c hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OM\) là trung trực của BC
\(\Rightarrow OM\perp BC\) tại H đồng thời H là trung điểm BC hay \(HB=HC\)
\(OC\perp MC\) (MC là tiếp tuyến tại C) \(\Rightarrow\Delta OMC\) vuông tại C
Áp dụng hệ thức lượng trong tam giác vuông OMC với đường cao CH:
\(CH^2=OH.MH\)
c.
C nằm trên đường tròn và AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\)
Xét hai tam giác MBH và BAC có:
\(\left\{{}\begin{matrix}\widehat{MHB}=\widehat{ACB}=90^0\\\widehat{MBH}=\widehat{BAC}\left(\text{cùng chắn BC}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBH\sim\Delta BAC\left(g.g\right)\)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{MH}{BC}\Rightarrow\dfrac{BH}{AC}=\dfrac{2HF}{2CH}\) (do F là trung điểm MH và H là trung điểm BC)
\(\Rightarrow\dfrac{BH}{AC}=\dfrac{HF}{CH}\)
Xét hai tam giác BHF và ACH có:
\(\left\{{}\begin{matrix}\dfrac{BH}{AC}=\dfrac{HF}{CH}\left(cmt\right)\\\widehat{BHF}=\widehat{ACH}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta BHF\sim\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{HBF}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{CBQ}\) (cùng chắn CQ)
\(\Rightarrow\widehat{HBF}=\widehat{CBQ}\) hay \(\widehat{HBF}=\widehat{HBQ}\)
\(\Rightarrow B,Q,F\) thẳng hàng
Đúng 2
Bình luận (0)
Cho đường tròn tâm (O), từ điểm M nằm ngoài đường tròn kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC với đường tròn, biết MA=6cm, MC=12cm.Tính MB.
Xét đường tròn tâm O ta có :
góc MAB = góc MCA = 1/2 sđ cung AB
Xét tam giác MAB và tam giác MCA có :
góc MAB = góc MCA
góc AMC Chung
=> \(\Delta MAB\sim\Delta MCA\)
=.> \(\dfrac{MA}{MC}=\dfrac{MB}{MA}\)
=> MA2=MC.MB
<=> 62=12.MB
=>MB =3cm
vậy MB = 3 cm
Đúng 3
Bình luận (0)
Cho điểm M nằm ngoài đường tròn O,bán kính R.Từ M kẻ hai tiếp tuyến MA,MB với đường tròn O(AB là các tiếp điểm ). Qua A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C. Nối MC cắt đường tròn (O;R) tại D. Tia AD cắt MB tại E. Chứng mình:
a. 4 điểm M,A,O,B cùng thuộc một đường tròn
b. EM=EB
giúp mình vs (vẽ hình nữa nha)
a) Xét tứ giác MAOB có
\(\widehat{OAM}\) và \(\widehat{OBM}\) là hai góc đối
\(\widehat{OAM}+\widehat{OBM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: M,A,O,B cùng thuộc một đường tròn(đpcm)
Đúng 1
Bình luận (0)
Cho đường tròn(O; R), điểm M nằm phía bên ngoài đường tròn sao cho OM = 2R. Từ điểm M kẻ các tiếp tuyến MB, MC với đường tròn (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OM và BC. a) Chứng minh: OM ⊥ BC tại H. b) Kẻ đường kính BD, chứng minh: CD//OM c) Tính MH.MO theo R. Tính 𝐵𝑀𝐶 = ? d) MD cắt đường tròn (O) tại điểm thứ hai là E. Chứng minh: MH.MO = ME.MD
Từ điểm M nằm ngoài đường tròn (O;R) kẻ các tiếp tuyến MA,MB của đường
tròn (O) (A và B là các tiếp điểm, OM 2R). Gọi E là trung điểm của đoạn thẳng MB,
C là giao điểm của đường thẳng AE với đường tròn (O) và tia MC cắt đường tròn (O)
tại điểm thứ hai D.
a) Chứng minh: tử giác MAOB nội tiếp và gócMOB gócADB;
b) Chứng minh: BF^2 EC EA và AD ||MB.
c) Kẻ đường kính BI của đường tròn (O). Đường thẳng MI và đường thẳng AD
cắt nhau tại K . Chứng minh: KD 3KA.
Đọc tiếp
Từ điểm M nằm ngoài đường tròn (O;R) kẻ các tiếp tuyến MA,MB của đường
tròn (O) (A và B là các tiếp điểm, OM > 2R). Gọi E là trung điểm của đoạn thẳng MB,
C là giao điểm của đường thẳng AE với đường tròn (O) và tia MC cắt đường tròn (O)
tại điểm thứ hai D.
a) Chứng minh: tử giác MAOB nội tiếp và gócMOB = gócADB;
b) Chứng minh: BF^2 = EC EA và AD ||MB.
c) Kẻ đường kính BI của đường tròn (O). Đường thẳng MI và đường thẳng AD
cắt nhau tại K . Chứng minh: KD = 3KA.
Làm giúp em phần a-b được thì c luôn ạ
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm M nằm ngoài đường tròn .Kẻ 2 tiếp tuyến MA , MB với đường tròn (O)
từ điểm A kẻ đường thẳng song song với MB cắt đường tròn tại C ,đường thẳng MC cắt đường tròn tại D
CMR : MD.MC=MA2
Xét ΔMAD và ΔMCA có
góc MAD=góc MCA
góc AMD chung
=>ΔMAD đồng dạng với ΔMCA
=>MA/MC=MD/MA
=>MA^2=MC*MD
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.b) Chứng minh: CH* OH.HM.
Đọc tiếp
Cho đường tròn (O; R) và một điểm M nằm ngoài đường tròn. Từ M kẻ các tiếp tuyến MB,
MC tới (O) (B, C là các tiếp điểm). Gọi H là giao điểm của MO với BC. Vẽ đường kính BA.
a) Chứng minh: Các điểm M, B, C, O cùng nằm trên một đường tròn.
b) Chứng minh: CH* = OH.HM.
a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MBOC là tứ giác nội tiếp
=>M,B,O,C cùng thuộc một đường tròn
b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)
Xét (O) có
MB,MC là các tiếp tuyến
Do đó: MB=MC
=>M nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra MO là đường trung trực của BC
=>MO\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot HM=HB^2\)
=>\(OH\cdot HM=HB\cdot HC\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) và một điểm A nằm bên ngoài đường tròn đó. Qua A kẻ đường thẳng d vuông góc với OA, trên đường thẳng d lấy một điểm M bất kì (M khác A). Từ M kẻ tiếp tuyến MB, MC tới đường tròn (O).
a) C/m tứ giác MBOC nội tiếp được đường tròn
b) MO cắt BC tại H, c/m OM.OH=R2
c) Khi điểm M thay đổi trên d, c/m BC luônđi qua một điểm cố định
a: Xét tứ giác MBOC có
\(\widehat{MBO}+\widehat{MCO}=180^0\)
Do đó: MBOC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
cho đường tròn (O) và điểm M nằm ngoài đường tròn .Kẻ 2 tiếp tuyến MA , MB với đường tròn (O)
từ điểm A kẻ đường thẳng song song với MB cắt đường tròn tại C ,đường thẳng MC cắt đường tròn tại D
CMR : đường thẳng AD đi qua trung điểm của MC