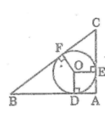
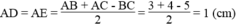Cho tam giác ABC vuông tại A nội tiếp đường tròn (O;R) có đường kính BC và cạnh AB=R. Kẻ dây AD vuông góc với BC tại H
a) Tính độ dài các cạnh AC,AH và số đo góc B, góc C
b) Chứng minh: AH.HD=HB.HC
c) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, căt AC ở N. Chứng minh: C,D,N thẳng hàng
d) Chứng minh: AI là tiếp tuyến của đường tròn (O) và tính AI theo R