Gía trị lớn nhất của hàm số y = - 2 4 - x là
A. -4
B. -2
C. 1
D. 0
Câu 1 : Cho hàm số y = f (x)= x2 - 1. Gía trị của f (-1) là:
A. -2 B. 0 C. -3 D. 1
Câu 2: Điểm thuộc đồ thị hàm số y = -2x là:
A. (-1; -2) B. (1/2; -4) C. (0;2) D. (-1; 2)
Câu 3: Cho biết x và y là hai đại lượng tỉ lệ thuận, biết khi x = 5 thì y = 15. Hệ số tỉ lệ của y đối với x là:
A. 1/3 B. 3 C. 75 D. 10
1/Giá trị nhỏ nhất của C=(x^2+13)^2
2/Gía trị lớn nhất của B=-(x-3)^2+5/4
3/ Gía trị của x để A=|x-1/3| nhỏ nhất
4/ Tổng các giá trị x thỏa mãn 3x^2-50x=0
Giá trị lớn nhất của hàm số sau trên khoảng (- ∞ ; + ∞ ) là:
y = 1 x 2 + x + 1
A. 1 B. 4/3
C. 5/3 D. 0
Đáp án: B.
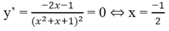
Bảng biến thiên
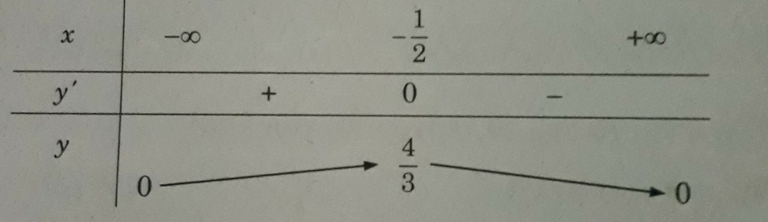
max y = 4/3
Tìm giá trị lớn nhất của hàm số sau trên [-1; 1]
![]()
A. max y = 0 B. max y = 2
C. max y = 4 D. max y = 2
Tập xác định -1 ≤ x ≤ 1, do đó 1 – x ≤ 2, 1 + x ≤ 2 ⇒ ( 1 - x ) + ( 1 + x ) ≤ 2 2 < 4 nên C sai; Ngoài ra vì 0 và 2 đều nhỏ hơn 2 nên chỉ cần xét xem 2 có phải là giá trị của hàm số không, dễ thấy khi x = 0 thì y = 2. Vậy max y = 2
Đáp án: B
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Gọi M,m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y=\(\sqrt{1+x}+\sqrt{1-x}\). Giá trị của M+m là
A.4 B.2+\(\sqrt{2}\) C.4+\(\sqrt{2}\) D.2
Giải thích hộ em với
Vẽ đồ thị hàm số y=(x)=-0,5.x :Hãy tính
A) f(2); f(-2); f(4); f(0)
B) Gía trị của x khi y=-1; y=0;y=2,5
LƯU Ý; LÀ HÃY TÍNH NHA CÁC BẠN
MÌNH CẦN GẤP:THANK BẠN
Tìm giá trị lớn nhất, giá trị lớn nhất của hàm số (nếu có)
a, \(y=\sqrt{x^2+x-2}\)
b, \(y=\sqrt{2+x}+\sqrt{4-x}\)
c, \(y=x+\sqrt{4-x^2}\)
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)
cho hàm số y = f(x) = 5 - 3x
a, tính f(-1) , f(0)
b, lập bang tính trị tương ứng của y khi x = -2 ,3
c, tính gía trị của x khi y = -4 , y = 0
ai làm nhanh mik tick nha