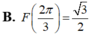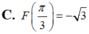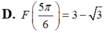Đáp án: B.
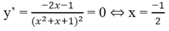
Bảng biến thiên
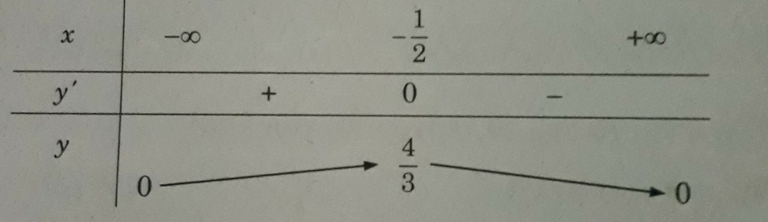
max y = 4/3
Đáp án: B.
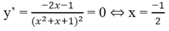
Bảng biến thiên

max y = 4/3
Giá trị lớn nhất của hàm số sau trên khoảng (- ∞ ; + ∞ ) là:
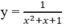
A. 1 B. 4/3
C. 5/3 D. 0
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π /2) là:
y = 1 sinx + cosx
A. 1 B. 2 2
C. - 2 D. 2 /2
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Giá trị lớn nhất của hàm số y = - x 2 + 4x - 5 trên đoạn [0;3] bằng:
A. -1 B. 1
C. 2 D. 0
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?