Cho hàm số y = 2 x - 1 x - 1 ( C ) . Hệ số góc của tiếp tuyến với đồ thị sao cho tiếp tuyến đó cắt trục Ox , Oy lần lượt tại các điểm A , B thỏa mãn OA=4OB là:
A. - 1 4
B. 1 4
C. - 1 4 hoặc 1 4
D. 1
Cho hàm số y = (2 - x)/(x - 1) (H.16) có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
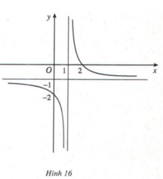
Khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞ dần tiến về 0.
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Với các hàm số bậc nhất, hãy cho biết hàm số đó đồng biến hay nghịch biến? a)y=5-2x b)y=x√2-1. C)y=2(x+1)-2x. D)y=3(x-1)x. e)y=-2/3 x. f)y=x+ 1/x
Các hàm số a,b,e là các hàm số bậc nhất
Trong các hàm số sau,hàm số nào là hàm số bậc nhất ? Với các hàm số bậc nhất , hãy cho biết hàm số đó đồng biến hay nghịch biến ?
a) y = 5 - 2x b) y = x√2 -1 c) y = 2(x+1) - 2x
d) y = 3(x-1) - x e) y = -2/3x f) y= x + 1/x
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
Tính đạo hàm của các hàm số sau:
a) \(y = (2x^2 - x + 1)^{\frac{1}{3}}\)
b) \(y = (3x+1)^{\pi}\)
c) \(y = \sqrt[3]{\dfrac{1}{x-1}}\)
d) \(y =\log_{3} \left(\dfrac{x+1}{x-1}\right)\)
e) \(y = 3^{x^{2}}\)
f) \(y = \left(\dfrac{1}{2}\right)^{x^2-1}\)
h) \(y = (x+1) . e^{cosx}\)
g) \(y = \ln (x^2+x+1)\)
l) \(y = \dfrac{\ln x}{x+1}\)
a: \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
=>\(y'=\dfrac{1}{3}\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}\cdot\left(2x^2-x+1\right)'\)
\(=\dfrac{1}{3}\cdot\left(4x-1\right)\left(2x^2-x+1\right)^{-\dfrac{2}{3}}\)
b: \(y=\left(3x+1\right)^{\Omega}\)
=>\(y'=\Omega\cdot\left(3x+1\right)'\cdot\left(3x+1\right)^{\Omega-1}\)
=>\(y'=3\Omega\left(3x+1\right)^{\Omega-1}\)
c: \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
=>\(y'=\dfrac{\left(\dfrac{1}{x-1}\right)'}{3\cdot\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(=\dfrac{\dfrac{1'\left(x-1\right)-\left(x-1\right)'\cdot1}{\left(x-1\right)^2}}{\dfrac{3}{\sqrt[3]{\left(x-1\right)^2}}}\)
\(=\dfrac{-x}{\left(x-1\right)^2}\cdot\dfrac{\sqrt[3]{\left(x-1\right)^2}}{3}\)
\(=\dfrac{-x}{\sqrt[3]{\left(x-1\right)^4}\cdot3}\)
d: \(y=log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Leftrightarrow y'=\dfrac{\left(\dfrac{x+1}{x-1}\right)'}{\dfrac{x+1}{x-1}\cdot ln3}\)
\(\Leftrightarrow y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}:\dfrac{ln3\left(x+1\right)}{x-1}\)
\(\Leftrightarrow y'=\dfrac{x-1-x-1}{\left(x-1\right)^2}\cdot\dfrac{x-1}{ln3\cdot\left(x+1\right)}\)
\(\Leftrightarrow y'=\dfrac{-2}{\left(x-1\right)\cdot\left(x+1\right)\cdot ln3}\)
e: \(y=3^{x^2}\)
=>\(y'=\left(x^2\right)'\cdot ln3\cdot3^{x^2}=2x\cdot ln3\cdot3^{x^2}\)
f: \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
=>\(y'=\left(x^2-1\right)'\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}=2x\cdot ln\left(\dfrac{1}{2}\right)\cdot\left(\dfrac{1}{2}\right)^{x^2-1}\)
h: \(y=\left(x+1\right)\cdot e^{cosx}\)
=>\(y'=\left(x+1\right)'\cdot e^{cosx}+\left(x+1\right)\cdot\left(e^{cosx}\right)'\)
=>\(y'=e^{cosx}+\left(x+1\right)\cdot\left(cosx\right)'\cdot e^u\)
\(=e^{cosx}+\left(x+1\right)\cdot\left(-sinx\right)\cdot e^u\)
a) \(y=\left(2x^2-x+1\right)^{\dfrac{1}{3}}\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{\dfrac{1}{3}-1}.\left(4x-1\right)\)
\(\Rightarrow y'=\dfrac{1}{3}.\left(2x^2-x+1\right)^{-\dfrac{2}{3}}.\left(4x-1\right)\)
b) \(y=\left(3x+1\right)^{\pi}\)
\(\Rightarrow y'=\pi.\left(3x+1\right)^{\pi-1}.3=3\pi.\left(3x+1\right)^{\pi-1}\)
c) \(y=\sqrt[3]{\dfrac{1}{x-1}}\)
\(\Rightarrow y'=\dfrac{\left(x-1\right)^{-1-1}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^{3-1}}}=\dfrac{\left(x-1\right)^{-2}}{3\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}=\dfrac{1}{3.\sqrt[]{x-1}.\sqrt[3]{\left(\dfrac{1}{x-1}\right)^2}}\)
\(\Rightarrow y'=\dfrac{1}{3\left(x-1\right)^{\dfrac{1}{2}}.\left(x-1\right)^{\dfrac{2}{3}}}=\dfrac{1}{3\left(x-1\right)^{\dfrac{7}{6}}}=\dfrac{1}{3\sqrt[6]{\left(x-1\right)^7}}\)
d) \(y=\log_3\left(\dfrac{x+1}{x-1}\right)\)
\(\Rightarrow y'=\dfrac{\dfrac{1-\left(-1\right)}{\left(x-1\right)^2}}{\dfrac{x+1}{x-1}.\ln3}=\dfrac{2}{\left(x+1\right)\left(x-1\right).\ln3}\)
e) \(y=3^{x^2}\)
\(\Rightarrow y'=3^{x^2}.ln3.2x=2x.3^{x^2}.ln3\)
f) \(y=\left(\dfrac{1}{2}\right)^{x^2-1}\)
\(\Rightarrow y'=\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}.2x=2x.\left(\dfrac{1}{2}\right)^{x^2-1}.ln\dfrac{1}{2}\)
Các bài còn lại bạn tự làm nhé!
Cho hàm số y=f(x)=x; y=g(x)=-2x; y=h(x)=1; y=k(x)=5; y=z(x)=\(\frac{1}{x}\); y=t(x)=\(^{x^2}\). Trong các hàm số trên, hàm số nào có tính chất f(-x)=f(x)
Ảnh đẹp thì
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Bải 1: Tìm tập xác định của các hàm số
sau:
a)
3x-2
2x+1
c) y=\sqrt{2x+1}-\sqrt{3-x}
b) y=
²+2x-3
d) y=
√2x+1
X
f(x)
Chú ý: * Hàm số cho dạng v
thi f(x) * 0.
ở Hàm số cho dạng y = v/(x) thì f(r) 2 0.
X
* Hàm số cho dạng " J7(p) thi f(x)>0.
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Bài 1 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 2 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 3 : Cho hàm số: y= f(x)= a.x2+b.x+c cho biết f(0)=2010, f(1)=2011, f(-1)=2012, Tính f(-2).
Bài 4 : Cho đa thức: f(x)= x2-a.x-3 và g(x)= (x3-x2-x-a-1)2015
a, Tìm a biết -1 là 1 nghiệm của f(x)
b, Với a tìm được ở câu a, Tìm nghiệm còn lại của f(x) và tính g(2).
Bài 5: Cho hàm số y= f(x)= a.x2+b.x+c và biết f(0)=2014, f(1)=2015, f(-1)=2017 ,
Tính f(-2).
Mọi người giúp mình với ạ mình đang cần gấp. Mình cảm ơn mọi người nhiều.
Bài 1 : làm tương tự với bài 2;3 nhé
Ta có : \(f\left(0\right)=c=2010;f\left(1\right)=a+b+c=2011\)
\(\Rightarrow f\left(1\right)=a+b=1\)
\(f\left(-1\right)=a-b+c=2012\Rightarrow f\left(-1\right)=a-b=2\)
\(\Rightarrow a+b=1;a-b=2\Rightarrow2a=3\Leftrightarrow a=\dfrac{3}{2};b=\dfrac{3}{2}-2=-\dfrac{1}{2}\)
Vậy \(f\left(-2\right)=4a-2b+c=\dfrac{4.3}{2}-2\left(-\dfrac{1}{2}\right)+2010=6+1+2010=2017\)
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020