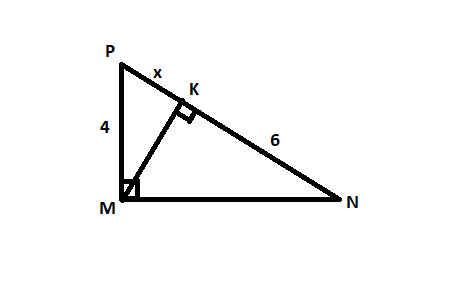
Cho tam giác MNP vuông tại M, MK là đường cao, biết MP = 4cm, PK = x, NK = 6. Tìm x
Xét ΔMNP vuông tại M có MK là đường cao
nên \(PM^2=PK\cdot PN\)
=>x(x+6)=16
=>x=2
Đúng 2
Bình luận (0)
Xét `\triangle MNP` vuông tại `M` có: `MK` là đường cao
`=>MP^2=PK.PN` (Ht giữa cạnh và đường cao)
`=>MP^2=PK.(PK+KN)`
`=>4^2=x(x+6)`
`<=>x^2+6x-16=0`
`<=>(x+8)(x-2)=0`
`<=>` $\left[\begin{matrix} x=-8\text{ (ko t/m)}\\ x=2\text{ (t/m)}\end{matrix}\right.$
Vậy `x=2`
Đúng 2
Bình luận (0)
cho tam giác vuông MNP tại M, đường cao MK. Biết MN= 7cm, NP= 25cm. Tính MP, MK, NK
Áp dụng định lý Py-ta-go cho tam giác MNP vuông tại M:
\(MN^2+MP^2=NP^2\)
Thay số: \(7^2+MP^2=25^2\)
\(\Rightarrow MP=24\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông MNP, đường cao MH ta có:
\(MK.NP=MN.MP\)
Thay số: \(MK.25=7.24\Rightarrow MK=6,72\left(cm\right)\)
Áp dụng định lý Py - ta - go cho tam giác MNK vuông tại K ta có:
\(MK^2+NK^2=MN^2\)
Thay số: \(6,72^2+NK^2=7^2\Rightarrow NK=1,96cm\)
Đúng 3
Bình luận (1)
Cho tam giác MNP vuông ở M và có đường cao MK a. - Chứng minh tam giác KNM đồng dạng với tam giác MNP đồng dạng tam giác KMP b. - Chứng minh MK2 = NK.KP c. - Tính MK, diện tích tam giác MNP . Biết NK = 4cm, KP = 9cm
a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
\(\widehat{N}\) chung
Do đó: ΔKNM~ΔMNP
Xét ΔMNP vuông tại M và ΔKMP vuông tại K có
\(\widehat{P}\) chung
Do đó: ΔMNP~ΔKMP
=>ΔKNM~ΔMNP~ΔKMP
b: Ta có: ΔKNM~ΔKMP
=>\(\dfrac{KN}{KM}=\dfrac{KM}{KP}\)
=>\(KM^2=KN\cdot KP\)
c: ta có: NP=NK+KP
=4+9
=13(cm)
Ta có: \(KM^2=KN\cdot KP\)
=>\(KM^2=4\cdot9=36\)
=>\(KM=\sqrt{36}=6\left(cm\right)\)
Xét ΔMNP vuông tại M có MK là đường cao
nên \(S_{MNP}=\dfrac{1}{2}\cdot MK\cdot PN=\dfrac{1}{2}\cdot6\cdot13=39\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông ở M và có đường cao MK a. - Chứng minh tam giác KNM đồng dạng với tam giác MNP đồng dạng tam giác KMP b. - Chứng minh MK2 = NK.KP c. - Tính MK, diện tích tam giác MNP . Biết NK = 4cm, KP = 9cm
a: Xét ΔKNM vuông tại K và ΔMNP vuông tại M có
góc N chung
=>ΔKNM đồng dạng với ΔMNP
Xét ΔKMP vuông tại K và ΔMNP vuông tại M có
góc P chung
=>ΔKMP đồng dạng với ΔMNP
b: ΔKNM đồng dạng với ΔKMP
=>KN/KM=KM/KP
=>KM^2=KN*KP
c: \(MK=\sqrt{4\cdot9}=6\left(cm\right)\)
\(S_{MNP}=\dfrac{1}{2}\cdot6\cdot13=3\cdot13=39\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M và đường cao MK
Tinh MK, dien tich tam giac MND biet NK=4cm KP= 9cm
Cho tam giác vuông MNP vuông tại M. Đường cao MI cắt cạnh NP thành hai đoạn là NI=4, IP=9
A, Tính MN, MP, MI, góc N, góc P.
B, Vẽ phân giác NK. Tính MK và KP.
C, Gọi G là giao điểm của NK và MI. Cm tam giác MGK cân.
cho tam giác MNP vuông tại M có MK đường cao.biết MP = 10 cm, KP = 8 cm .Tính MK, NK, MN
Xem chi tiết
Áp dụng hệ thức trong tam giác vuông có:
\(MP^2=PK.PN\Leftrightarrow PN=12,5\left(cm\right)\)
\(MN=\sqrt{PN^2-MP^2}=7,5cm\)
\(MN^2=NK.NP\Leftrightarrow NK=4,5\left(cm\right)\)
\(MK^2=KN.KP=4,5.8=36\Leftrightarrow MK=6\left(cm\right)\)
Vậy...
Đúng 1
Bình luận (0)
NP=MP^2/PN=10^2/8=12,5cm
MK=căn 10^2-8^2=6cm
NK=6^2/8=4,5cm
MN=căn 12,5^2-10^2=7,5cm
Đúng 0
Bình luận (0)
`@`Phamdanhv.
ảnh mình không tải được , bạn vào link này nhé
`=>`
blob:https://www.facebook.com/87ade4e1-6c0b-45ee-b42f-df163ba3224e
Đúng 0
Bình luận (0)
cho tam giác MNP vuông tại M kẻ đường cao MH, đường phân giác MK của góc HMP, kẻ đường cao KE vuông góc MP tại E. tính MN biết NP=12cm, KE=3cm
Cho tam giác MNP vuông tại M đường cao MK, biết MN = 9cm; NP = 15cm. Tính KN?
Áp dụng HTL: \(KN=\dfrac{MN^2}{NP}=5,4\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác MNP vuông ở N, phân giác ME. Gọi H là hình chiếu của E trên đường thẳng MP. Đường thẳng EH cắt MN kéo dài tại I. Kẻ NK là đường cao của tam giác MNP.
Hỏi: Tam giác MNP cần thêm điều kiện gì để E là trọng tâm của tam giác MIP.





