Xét ΔMNP vuông tại M có MK là đường cao
nên \(PM^2=PK\cdot PN\)
=>x(x+6)=16
=>x=2
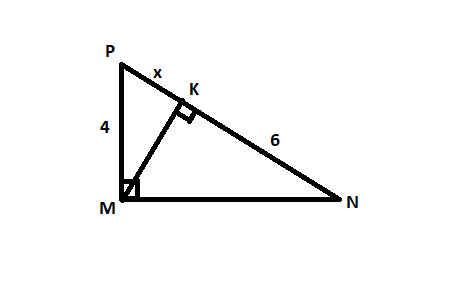
Xét `\triangle MNP` vuông tại `M` có: `MK` là đường cao
`=>MP^2=PK.PN` (Ht giữa cạnh và đường cao)
`=>MP^2=PK.(PK+KN)`
`=>4^2=x(x+6)`
`<=>x^2+6x-16=0`
`<=>(x+8)(x-2)=0`
`<=>` $\left[\begin{matrix} x=-8\text{ (ko t/m)}\\ x=2\text{ (t/m)}\end{matrix}\right.$
Vậy `x=2`


