Tìm tọa độ A’ đối xứng với A(1,-2,3) qua đường thẳng d : x - 1 1 = y - 1 = z - 2 1 .
![]()
![]()
![]()
![]()
Bài 1: Trong htđ Oxy cho đường thẳng d : 3x-y+4 = 0 và đường thẳng denta : x+2y-5=0 .
Điểm A ( -2; 3).
1) Hãy tìm tọa độ điểm H là hình chiếu của A trên d.
2) tìm tọa độ A’ là điểm đối xứng với A qua d.
3) Viết phương trình đường thẳng đối xứng với đường thẳng d qua đường thẳng denta
4) Viết phuong trình đường thẳng đôi xứng với d qua A ( 3 dạng PT).
5) Tìm tọa độ điểm N trên d sao cho ON nhỏ nhất.
P/S : GIÚP MK VS Ạ. MK CẦN LẮM Ạ. GIẢI CHI TIẾT GIÚP MK VS Ạ. THANKS NHÌU NHÌU Ạ
1. Gọi d' là đường thẳng qua A và vuông góc d
\(\Rightarrow\) d' nhận (1;3) là 1 vtpt
Phương trình d':
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-4=0\)
H là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+3y-4=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{5}\\y=\dfrac{8}{5}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
2.
Do A' đối xứng A qua d nên H là trung điểm AA'
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=\dfrac{2}{5}\\y_{A'}=2y_H-y_A=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow A'\left(\dfrac{2}{5};\dfrac{1}{5}\right)\)
3.
Gọi B là giao điểm d và \(\Delta\) thì tọa độ B thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{3}{7};\dfrac{19}{7}\right)\)
Lấy điểm \(C\left(0;4\right)\) thuộc d
Phương trình đường thẳng \(d_1\) qua C và vuông góc \(\Delta\) có dạng:
\(2\left(x-0\right)-\left(y-4\right)=0\Leftrightarrow2x-y+4=0\)
Gọi D là giao điểm \(\Delta\) và \(d_1\Rightarrow\left\{{}\begin{matrix}x+2y-5=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{14}{5}\right)\)
Gọi D' là điểm đối xứng C qua \(\Delta\Rightarrow\) D là trung điểm CD'
\(\Rightarrow\left\{{}\begin{matrix}x_{D'}=2x_D-x_C=-\dfrac{6}{5}\\y_{D'}=2y_D-y_C=\dfrac{8}{5}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BD'}=\left(-\dfrac{27}{35};-\dfrac{39}{35}\right)=-\dfrac{3}{35}\left(9;13\right)\)
Phương trình đường thẳng đối xứng d qua denta (nhận \(\left(9;13\right)\) là 1 vtcp và đi qua D':
\(\left\{{}\begin{matrix}x=-\dfrac{6}{5}+9t\\y=\dfrac{8}{5}+13t\end{matrix}\right.\)
4.
Gọi \(d_1\) là đường thẳng đối xứng với d qua A
\(\Rightarrow d_1||d\Rightarrow d_1\) có dạng: \(3x-y+c=0\)
Do A cách đều d và \(d_1\) nên:
\(d\left(A;d\right)=d\left(A;d_1\right)\)
\(\Leftrightarrow\dfrac{\left|3.\left(-2\right)-3+4\right|}{\sqrt{3^2+\left(-1\right)^2}}=\dfrac{\left|3.\left(-2\right)-3+c\right|}{\sqrt{3^2+\left(-1\right)^2}}\)
\(\Leftrightarrow\left|c-9\right|=5\Rightarrow\left[{}\begin{matrix}c=4\left(loại\right)\\c=14\end{matrix}\right.\)
Vậy pt \(d_1\) có dạng: \(3x-y+14=0\)
Em tự chuyển sang 2 dạng còn lại
Cho điểm A(1;0;0) và đường thẳng ∆ : x = 2 + t y = 1 + 2 t z = t Tìm tọa độ điểm A' đối xứng với A qua đường thẳng ∆
Vì A' là điểm đối xứng của A qua ∆ nên H là trung đểm của AA'.
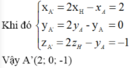
Trong không gian Oxyz, cho điểm A(1;0;-1) và đường thẳng d : x - 1 2 = y + 1 2 = z - 1 . Tọa độ điểm A’ đối xứng với A qua đường thẳng d là:
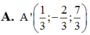
![]()
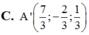
![]()
Đáp án C.
Đường thẳng d có véc tơ chỉ phương u → ( 2 ; 2 ; - 1 )
Gọi H(1+2t ;-1+2t ;-t) ∈ d là tọa độ hình chiếu vuông góc của A trên d.
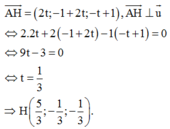
A’ đối xứng với A qua d ⇔ H là trung điểm của AA’
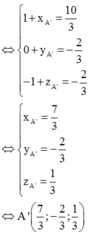
Tìm tọa độ điểm A' đối xứng với điểm A(1; -2; -5) qua đường thẳng có phương trình x = 1 + 2 t y = - 1 - t z = 2 t
Vecto chỉ phương của đường thẳng ∆ là a → = 2 ; - 1 ; 2
Ta có: M(1+2t;-1-t;2t) ∈ ∆
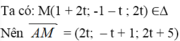
M là hình chiếu vuông góc của A trên ∆ khi:
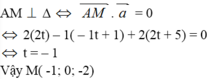
Vì A' đối xứng với A qua M nên M là trung điểm của AA'. Do đó, ta có: 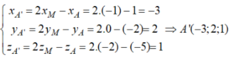
Cho điểm A ( 2;1) . Xác định tọa độ các điểm :
a) B đối xứng với A qua trục tung b) C đối xứng với A qua trục hoành
c) D dối xứng với A qua O d) E đối xứng với A qua đường thẳng d: y = 2x - 1
a: B đối xứng A qua trục tung Oy
=>\(\left\{{}\begin{matrix}x_B=-x_A=-2\\y_B=y_A=1\end{matrix}\right.\)
Vậy: B(-2;1)
b: C đối xứng A qua trục Ox
=>\(\left\{{}\begin{matrix}x_C=x_A=2\\y_C=-y_A=-1\end{matrix}\right.\)
Vậy: C(2;-1)
c: D đối xứng A qua O
=>O là trung điểm của AD
=>\(\left\{{}\begin{matrix}x_A+x_D=0\\y_A+y_D=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=-x_A=-2\\y_D=-y_A=-1\end{matrix}\right.\)
Vậy: D(-2;-1)
d: (d): y=2x-1
=>(d): 2x-y-1=0
E đối xứng A qua (d)
=>(d) là đường trung trực của AD
Gọi (d2): ax+by+c=0 là phương trình đường thẳng AD
(d) là trung trực của AD
=>(d) vuông góc (d2) tại trung điểm của AD(1) và (d2) đi qua A(2;1)
(d): 2x-y-1=0
=>(d2): x+2y+c=0
Thay x=2 và y=1 vào (d2), ta được:
\(c+2+2\cdot1=0\)
=>c=-4
=>(d2): x+2y-4=0
Tọa độ giao điểm F của (d) với (d2) là:
\(\left\{{}\begin{matrix}x+2y-4=0\\2x-y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2y=4\\2x-y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+4y=8\\2x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=7\\x+2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{7}{5}\\x=4-2y=4-\dfrac{14}{5}=\dfrac{6}{5}\end{matrix}\right.\)
(1) suy ra F là trung điểm của AE
=>\(\left\{{}\begin{matrix}\dfrac{6}{5}=\dfrac{x_A+x_E}{2}=\dfrac{2+x_E}{2}\\\dfrac{7}{5}=\dfrac{y_A+y_E}{2}=\dfrac{y_E+1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_E+2=\dfrac{12}{5}\\y_E+1=\dfrac{14}{5}\end{matrix}\right.\Leftrightarrow E\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
cho điểm m (-1 1) và đường thẳng denta 3x+y-8=0
a)Viết phương trình đường thẳng d đi qua m vuông góc với đường thẳng denta
b)Tìm tọa độ hình chiếu vuông góc với h của điểm M lên đường thẳng delta
c)tọa độ điểm M' đối xứng với điểm M Qua denta
a.
Do d vuông góc với \(\Delta\) nên d nhận \(\left(1;-3\right)\) là 1 vtpt
Phương trình d:
\(1\left(x+1\right)-3\left(y-1\right)=0\Leftrightarrow x-3y+4=0\)
b.
\(M\in d\) mà \(MH\perp\Delta\Rightarrow\) H là giao điểm của d và \(\Delta\)
Tọa độ H là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-3y+4=0\\3x+y-8=0\end{matrix}\right.\) \(\Rightarrow H\left(2;2\right)\)
c.
M' đối xứng với M qua \(\Delta\) khi và chỉ khi H là trung điểm MM'
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=5\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(5;3\right)\)
Tại sao lại đổi từ (3; 1) sang (1; -3 ) vậy ạ? Denlta có dạng pttq thì có vtpt và đường thẳng d cũng vuông góc với denlta rồi mà?
bài1 : cho △1: x+y-1=0 và△2:x-3y+3=0. Viết phương trình đường thẳng d đối xứng với đường thẳng△1qua đường thẳng △2
bài2:
cho đường thẳng △:2x-y+3=0 viết phương trình đường thẳng △':
a, đối xứng với △ qua Ox
b,đối xứng với △ qua Oy
c, đối xứng với △ qua gốc tọa độ O
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình lần lượt d: x = 1+2t, y = 2 - t, z = 3t . Tìm tọa độ điểm K đối xứng với điểm I(2;-1;3) qua đường thẳng d
A. K(4;3;3)
B. K(1;-3;3)
C. K(-4;-3;-3)
D. K(-1;3;-3)
Chọn A
Mặt phẳng qua I vuông góc với d có phương trình
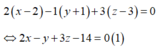
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào (1) ta có

Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : x - 2 3 = y - 1 - 1 = z + 1 1 và điểm A(1;2;3). Tọa độ điểm A' đối xứng với A qua d là
A. A'(3;1;-5)
B. A'(-3;0;5)
C. A'(3;0;-5)
D. A'(3;1;5)
Đường thẳng d có một VTCP u d → = 3 ; - 1 ; 1
Gọi α là mặt phẳng qua A và vuông góc với d nên có một VTPT
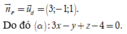
Tọa độ hình chiếu H của A trên d thỏa 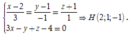
Khi đó H là trung điểm của AA' nên suy ra A'(3;0;-5). Chọn C.