Gọi M, N là giao điểm của đường thẳng y = x + 1 và đồ thị hàm số y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng:
A. − 5 2 .
B. 2
C. -1
D. 1
Gọi A là giao điểm của 2 đường thẳng y=-x+1 và y=x+3. Tìm số nguyên dương m để A thuộc đồ thị hàm số y = (m-1)x+m^2-1
Pt hoành độ giao điểm:
\(-x+1=x+3\Rightarrow2x=-2\)
\(\Rightarrow x=-1\Rightarrow y=x+3=2\)
\(\Rightarrow A\left(-1;2\right)\)
Để A thuộc \(y=\left(m-1\right)x+m^2-1\) thì:
\(-1.\left(m-1\right)+m^2-1=2\)
\(\Leftrightarrow m^2-m-2=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=2\end{matrix}\right.\)
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đồ thị hàm số y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. - 5 2
B. 2
C. -1
D. 1
Đáp án D
Xét pt tương giao:
x + 1 = 2 x + 4 x − 1 ⇔ ( x + 1 ) ( x − 1 ) = 2 x + 4 ⇔ x 2 − 2 x − 5 = 0 ⇔ x = 1 ± 6 ⇒ x I = 1
Gọi M, N là giao điểm của đường thẳng y = x+1 và đồ thị hàm số y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. − 5 2 .
B. 2.
C. -1.
D. 1.
Gọi M, N là các giao điểm của đường thẳng y = x − 4 với đồ thị của hàm số y = − 2 x + 5 x − 2 . Tìm tọa độ trung điểm I của MN?
A. I 2 ; − 2
B. I 1 ; − 3
C. I 3 ; − 1
D. I − 2 ; 2
Đáp án A
Hoành độ giao điểm là nghiệm của PT:
x − 4 = − 2 x + 5 x − 2 ⇔ x 2 − 6 x + 8 = − 2 x + 5 x ≠ 2
⇔ x 2 − 4 x − 13 = 0 . Vậy trung điểm I của MN có hoành độ x = 2 ⇒ y = − 2 .
cho hàm số y=x 4 và y=-x 2
a,vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b,gọi A là giao điểm của hai đường thẳng trên,B và C lần lượt là giao điểm của 2 đường thẳng đó với trục Ox.Tính chu vi và diện tích của tam giác ABC
Bạn nhập lại hai hàm số đó nhé chính giữa mik không biết là dấu + hay -
cho hai hàm số y= 2x-4 (d) và y = -x+4 (d')
a) vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ ?
b) Gọi giao điểm của đường thẳng (d) và(d') với trục Oy là N và M , giao điểm của hai đường thẳng là Q.
Xác định tỏa độ điểm Q và tính diện tích tam giác MNQ ? tính các góc của tam giác MNQ?
a:
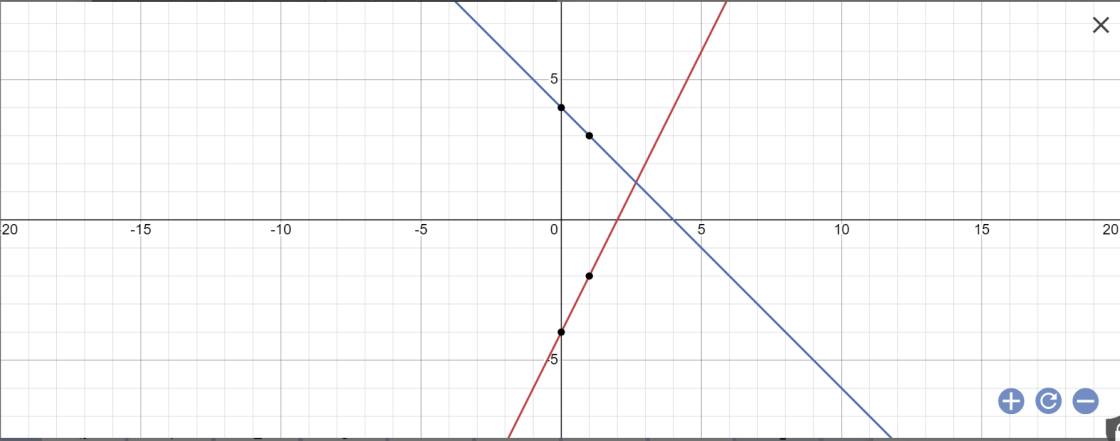
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
: Cho hàm số y = -x +1 , y = x+1 , y = -1
a) Vẽ trên cùng một hệ trục tọa độ , đồ thị các hàm số đó.
b) Gọi giao điểm của hai đường thẳng y = -x + 1 và y = x + 1 là A, giao điểm của đường thẳng y = -1 với hai đường thẳng trên là B , C . Chứng tỏ tam giác ABC là tam giac cân . Tính chu vi và diện tích tam giác ?
c) Tính góc tạo bởi đường thẳng y = x+1 với trục hoành
Cần giải gấp ạ . Cảm ơn ạ
Gọi M;N là giao điểm của đồ thị hàm số và đường thẳng y = x + 2 . Khi đó tung độ trung điểm I của đoạn MN bằng bao nhiêu?
A. − 3 2
B. 11 2
C. 7 2
D. − 7 2
Đáp án B
7 x + 6 x − 2 = x + 2 ⇔ x 2 − 4 = 7 x + 6 ⇔ x 2 − 7 x − 10 = 0 ⇒ x = 7 ± 89 2 ⇒ y = 11 ± 89 2
Suy ra: y I = y 1 + y 2 2 = 11 2 .
Chọn phương án B.
Gọi A, B là các giao điểm của đường thẳng y = -x + m và đồ thị hàm số y = x - 1 x . Khi đó tìm m để xA = xB = 1.
A. m = 2
B. m = 1
C. m = 3
D. m = 0
Chọn A.
Hoành độ A,B là nghiệm của pt ![]()
→ xA + xB = m – 1 = 1 ⇔ m = 2