Tìm tất cả giá trị của tham số m để hàm số y = x 3 + 3 x 2 + m x - 1 đồng biến trên R
A. m ≤ 3
B. m ≤ -3
C. m ≥ 3
D. m ≥ -3
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
cho hàm số y=x^2-3(m+1)x+m^2+3m-2, m là tham số . Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
Cho hàm số y= 2x^2 -3(m+1)x +m^2 +3m -2 , m là tham số . TÌm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất
cho hàm số y= \(\dfrac{1}{3}x^2\)-\(\dfrac{m}{2}+mx+5\)
tìm tất cả các giá trị của tham số m để y'≥0 ∀x∈R
Lời giải:
\(y'=\frac{2}{3}x+m\geq 0, \forall x\in\mathbb{R}\Leftrightarrow m\geq -\frac{2}{3}x, \forall x\in\mathbb{R}\)
\(\Leftrightarrow m\geq \max (\frac{-2}{3}x), \forall x\in\mathbb{R}\)
Vì $\frac{-2}{3}x$ không có max với mọi $x\in\mathbb{R}$ nên không tồn tại $m$
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số \(y=x^3-3x^2+mx+1\) đạt cực tiểu tại x=2
Tìm tất cả giá trị thực của tham số m để hàm số \(y=\sqrt{\left(m-2\right)x+2m-3}\) xác định với mọi x ∈ [-1; 4]
Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)
\(\Leftrightarrow mx-2x+2m-3\ge0\)
\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)
\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)
\(\Rightarrow1\le m\le\dfrac{11}{6}\)
Tìm tất cả các giá trị của tham số m để hàm số y = 1 m log 3 2 x - 4 log 3 x + m + 3 xác định trên khoảng ( 0 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
B . m ∈ ( 1 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
C . m ∈ ( - ∞ ; - 4 )
Chọn A
Cách 1
Điều kiện: x > 0
Hàm số xác định khi:
![]()
![]()
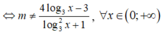
Để hàm số xác định trên
(
0
;
+
∞
)
thì phương trình 
Xét hàm số 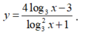
Đặt ![]() khi đó ta có
khi đó ta có
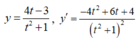
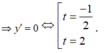
Ta có BBT:
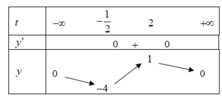
Để hàm số xác định trên ![]()
Cách 2:
Đề hàm số xác định trên khoảng ![]() thi phương trình
thi phương trình ![]() vô nghiệm.
vô nghiệm.
TH1: m = 0 thì PT trở thành ![]()
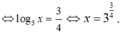
Vậy m = 0 không thỏa mãn.
TH2:
m
≠
0 thì để PT vô nghiệm ![]()
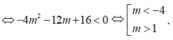
Để hàm số xác định trên ![]()
tìm tập tất cả các giá trị của tham số m để hàm số y= -1/3x^3-(m-2)x^2+(m-2)x+m luôn nghịch biến trên tập xác định
\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)