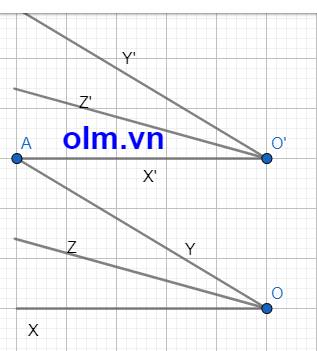
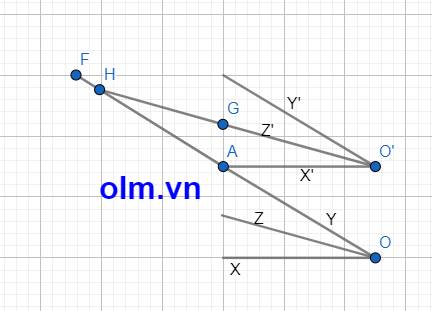
Cho hai góc x O z ^ , y O z ^ kề bù. Biết y O z ^ = 60 0
a) Tính x O z ^ ?
b) Gọi Om là tia phân giác của x O z ^ ? . Tính y O m ^
c) Chứng minh Oz là tia phân giác của y O m ^
d) Gọi On là tia phân giác của y O z ^ . Tính m O n ^
e) Trong bốn góc x O y ^ , y O z ^ , m O n ^ , x O z ^ góc nào là goc nhọn, tù, vuông, bẹt? Vì sao?