Tích phân ∫ 0 1 1 cos 2 x d x bằng
A. tan1.
B. -cot1.
C. -tan1.
D. cot1.
a.3 cos x-3 + sin 2x(1-cosx)=0
b.cos 2x+sin x+cos x=0
c.sin 4x-2 cos2x=0
d.(3sin x-2)(cos x-1)=0
Tính các tích phân sau :
a) \(\int\limits^{\dfrac{\pi}{4}}_0\cos2x.\cos^2xdx\)
b) \(\int\limits^1_{\dfrac{1}{2}}\dfrac{e^x}{e^{2x}-1}dx\)
c) \(\int\limits^1_0\dfrac{x+2}{x^2+2x+1}\ln\left(x+1\right)dx\)
d) \(\int\limits^{\dfrac{\pi}{4}}_0\dfrac{x\sin x+\left(x+1\right)\cos x}{x\sin x+\cos x}dx\)
a)
Ta có \(A=\int ^{\frac{\pi}{4}}_{0}\cos 2x\cos^2xdx=\frac{1}{4}\int ^{\frac{\pi}{4}}_{0}\cos 2x(\cos 2x+1)d(2x)\)
\(\Leftrightarrow A=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos x(\cos x+1)dx=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos xdx+\frac{1}{8}\int ^{\frac{\pi}{2}}_{0}(\cos 2x+1)dx\)
\(\Leftrightarrow A=\frac{1}{4}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin x+\frac{1}{16}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin 2x+\frac{1}{8}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|x=\frac{1}{4}+\frac{\pi}{16}\)
b)
\(B=\int ^{1}_{\frac{1}{2}}\frac{e^x}{e^{2x}-1}dx=\frac{1}{2}\int ^{1}_{\frac{1}{2}}\left ( \frac{1}{e^x-1}-\frac{1}{e^x+1} \right )d(e^x)\)
\(\Leftrightarrow B=\frac{1}{2}\left.\begin{matrix} 1\\ \frac{1}{2}\end{matrix}\right|\left | \frac{e^x-1}{e^x+1} \right |\approx 0.317\)
c)
Có \(C=\int ^{1}_{0}\frac{(x+2)\ln(x+1)}{(x+1)^2}d(x+1)\).
Đặt \(x+1=t\)
\(\Rightarrow C=\int ^{2}_{1}\frac{(t+1)\ln t}{t^2}dt=\int ^{2}_{1}\frac{\ln t}{t}dt+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
\(=\int ^{2}_{1}\ln td(\ln t)+\int ^{2}_{1}\frac{\ln t}{t^2}dt=\frac{\ln ^22}{2}+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=\frac{dt}{t^2}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=\frac{-1}{t}\end{matrix}\right.\Rightarrow \int ^{2}_{1}\frac{\ln t}{t^2}dt=\left.\begin{matrix} 2\\ 1\end{matrix}\right|-\frac{\ln t+1}{t}=\frac{1}{2}-\frac{\ln 2 }{2}\)
\(\Rightarrow C=\frac{1}{2}-\frac{\ln 2}{2}+\frac{\ln ^22}{2}\)
d)
\(D=\int ^{\frac{\pi}{4}}_{0}\frac{x\sin x+(x+1)\cos x}{x\sin x+\cos x}dx=\int ^{\frac{\pi}{4}}_{0}dx+\int ^{\frac{\pi}{4}}_{0}\frac{x\cos x}{x\sin x+\cos x}dx\)
Ta có:
\(\int ^{\frac{\pi}{4}}_{0}dx=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|x=\frac{\pi}{4}\)
\(\int ^{\frac{\pi}{4}}_{0}\frac{x\cos xdx}{x\sin x+\cos x}=\int ^{\frac{\pi}{4}}_{0}\frac{d(x\sin x+\cos x)}{x\sin x+\cos x}=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\ln |x\sin x+\cos x|\)
\(=\ln|\frac{\pi\sqrt{2}}{8}+\frac{\sqrt{2}}{2}|\)
Suy ra \(D=\frac{\pi}{4}+\ln|\frac{\pi\sqrt{2}}{8}+\frac{\sqrt{2}}{2}|\)
Chứng minh rằng với \(0^0\le x\le180^0\) ta có :
a) \(\left(\sin x+\cos x\right)^2=1+2\sin x\cos x\)
b) \(\left(\sin x-\cos x\right)^2=1-2\sin x\cos x\)
c) \(\sin^4x+\cos^4x=1-2\sin^2x\cos^2x\)
a) \(\left(sinx+cosx\right)^2=sin^2x+2sinxcosx+cos^2x\)\(=1+2sinxcosx\).
b) \(\left(sinx-cosx\right)^2=sin^2x-2sinxcosx+cos^2x\)\(=1-2sinxcosx\).
c) \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\).
Đưa về tích rồi giải các phương trình sau:
a) \(\sin 2x -2.\sin x +\cos x -1=0\)
b) \(\sqrt{2} . (\sin x - 2.\cos x) = 2-\sin 2x\)
c) \(\frac{1}{\cos x} - \frac{1}{\sin x}=2\sqrt 2 .\cos(x + \frac{\pi}{4}) \)
\(a,sin2x-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinxcosx-2sinx+cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx-1\right)+cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=1\\sinx=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2k\pi\\x=\frac{-\pi}{6}+2k\pi\end{cases}}}\)
\(b,\sqrt{2}\left(sinx-2cosx\right)=2-sin2x\)
\(\Leftrightarrow\sqrt{2}sinx-2\sqrt{2}cosx-2+2sinxcosx=0\)
\(\Leftrightarrow\sqrt{2}sinx\left(1+\sqrt{2}cosx\right)-2.\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}cosx+1\right)\left(\sqrt{2}sinx-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=\frac{-\sqrt{2}}{2}\\sinx=\frac{2\sqrt{2}}{2}\left(l\right)\end{cases}}\)(vì \(-1\le sinx\le1\))
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3\pi}{4}+2k\pi\\x=\frac{5\pi}{4}+2k\pi\end{cases}}\)
\(c,\frac{1}{cosx}-\frac{1}{sinx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{sinx-cosx}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{-\sqrt{2}cos\left(x+\frac{\pi}{4}\right)}{sinx.cosx}=2\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow sin2x+1=0\)
\(\Leftrightarrow sin2x=-1\)
\(\Leftrightarrow2x=\frac{3\pi}{2}+2k\pi\)
\(\Leftrightarrow x=\frac{3\pi}{4}+k\pi\)
@Bùi Nhật Vy, Bạn nhớ kĩ cái này nha
\(asinx+bcosx=\sqrt{a^2+b^2}sin\left(x+\alpha\right)=-\sqrt{a^2+b^2}cos\left(x-\alpha\right)\)
trong đó \(\cos\alpha=\frac{a}{\sqrt{a^2+b^2}},sin\alpha=\frac{b}{\sqrt{a^2+b^2}}\)
Giải phương trình lượng giác sau
1) 2 cos 2x -\(\sqrt{3}\) = 0
2)\(\sqrt{3}\) tan x + 1 = 0
3) 2 cos2x = 1
4) 6 sin2 x- 13 sin x + 5 = 0
5) 5 cos 2x + 6 cos x + 1 = 0
6 ) 2 cos 2 2x - 3 cos 2x + 1 = 0
7) tan 2 x + ( 1 - \(\sqrt{3}\)) tan x - \(\sqrt{3}\) = 0
8) cos 6x + 2 sin 3x + 3 = 0
9) cos 2x - 4 cos x - 5 = 0
10 ) 3 cos 2 x = 2 sin 2 x + 4 sin x
11) cos 2x + sin2x + 2 cos x + 1 = 0
12) cos 4x + sin 4x + sin 2x = \(\dfrac{5}{2}\)
Tìm số đo góc nhọn x:
a) \(4\sin x-1=1\)
b) \(2\sqrt{3}-3\tan x=\sqrt{3}\)
c) \(7\sin-3\cos\left(90^o-x\right)=2,5\)
d) \(\left(2\sin-\sqrt{2}\right)\left(4\cos-5\right)=0\)
e) \(\dfrac{1}{\cos^2x}-\tan x=1\)
f) \(\cos^2x-3\sin^2x=0,19\)
a) \(4sinx-1=1\Leftrightarrow4sinx=2\Leftrightarrow sinx=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow x=30^o\)
b) \(2\sqrt{3}-3tanx=\sqrt{3}\Leftrightarrow3tanx=2\sqrt{3}-\sqrt{3}=\sqrt{3}\Leftrightarrow tanx=\dfrac{\sqrt{3}}{3}\)
\(\Leftrightarrow x=30^o\)
c) \(7sinx-3cos\left(90^o-x\right)=2,5\Leftrightarrow7sinx-3sinx=2,5\Leftrightarrow4sinx=2,5\Leftrightarrow sinx=\dfrac{5}{8}\Leftrightarrow x=30^o41'\)
d)\(\left(2sin-\sqrt{2}\right)\left(4cos-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2sin-\sqrt{2}=0\\4cos-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}2sin=\sqrt{2}\\4cos=5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}sin=\dfrac{\sqrt{2}}{2}\\cos=\dfrac{5}{4}\left(loai\right)\end{matrix}\right.\)\(\Rightarrow x=45^o\)
Xin lỗi nãy đang làm thì bấm gửi, quên còn câu e, f nữa:"(
e) \(\dfrac{1}{cos^2x}-tanx=1\Leftrightarrow1+tan^2x-tanx-1=0\Leftrightarrow tan^2x-tanx=0\Leftrightarrow tanx\left(tanx-1\right)=0\Rightarrow tanx-1=0\Leftrightarrow tanx=1\Leftrightarrow x=45^o\)
f) \(cos^2x-3sin^2x=0,19\Leftrightarrow1-sin^2x-3sin^2x=0,19\Leftrightarrow1-4sin^2x=0,19\Leftrightarrow4sin^2x=0,81\Leftrightarrow sin^2x=\dfrac{81}{400}\Leftrightarrow sinx=\dfrac{9}{20}\Leftrightarrow x=26^o44'\)
1. Cho A = \(x^2-3x\sqrt{y}+2y\)
a) Phân tích A thành phân tử
b) Tìm A khi \(x=\frac{1}{\sqrt{5}-2};y=\frac{1}{9+4\sqrt{5}}\)
2. Rút gọn
a) A = \(\frac{1+2\sin x.\cos x}{\sin x+\cos x}\)
b) B = \(\cot x+\frac{\sin x}{1+\cos x}\)
Giải PT
a) 4sin (3x + \(\frac{\pi}{3}\)) - 2 = 0
b) 4sin ( 4x + 1) -1 = 0
c) sin ( x + \(\frac{x}{4}\)) -1 = 0
d) 2sin ( 2x + 70o) + 1 = 0
e) sin x . cos ( 2x - 3 ) = 0
f) cos 2x -cos 4x = 0
g) cos ( sin 3x) = 1
a)
\(4\sin (3x+\frac{\pi}{3})-2=0\Leftrightarrow \sin (3x+\frac{\pi}{3})=\frac{1}{2}=\sin (\frac{\pi}{6})\)
\(\Rightarrow \left[\begin{matrix} 3x+\frac{\pi}{3}=\frac{\pi}{6}+2k\pi \\ 3x+\frac{\pi}{3}=\pi-\frac{\pi}{6}+2k\pi\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} x=\frac{-\pi}{18}+\frac{2\pi}{3}\\ x=\frac{\pi}{6}+\frac{2\pi}{3}\end{matrix}\right.\) (k nguyên)
c)
\(\sin (x+\frac{x}{4})-1=0\Leftrightarrow \sin (\frac{5}{4}x)=1=\sin (\frac{\pi}{2})\)
\(\Rightarrow \frac{5}{4}x=\frac{\pi}{2}+2k\pi\Rightarrow x=\frac{2}{5}\pi+\frac{8}{5}k\pi \) (k nguyên)
d)
\(2\sin (2x+70^0)+1=0\Leftrightarrow \sin (2x+\frac{7}{18}\pi)=-\frac{1}{2}=\sin (\frac{-\pi}{6})\)
\(\Rightarrow \left[\begin{matrix} 2x+\frac{7}{18}\pi=\frac{-\pi}{6}+2k\pi\\ 2x+\frac{7}{18}\pi=\frac{7}{6}\pi+2k\pi\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} x=\frac{-5\pi}{18}+k\pi\\ x=\frac{7}{18}\pi+k\pi\end{matrix}\right.\)
f)
\(\cos 2x-\cos 4x=0\)
\(\Leftrightarrow \cos 2x=\cos 4x\Rightarrow \left[\begin{matrix} 4x=2x+2k\pi\\ 4x=-2x+2k\pi\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix} x=k\pi\\ x=\frac{k}{3}\pi \end{matrix}\right.\) ( k nguyên)
b,e,g bạn xem lại đề, đơn vị không thống nhất.
Giải các phương trình sau :
a) \(\sin^2\dfrac{x}{2}-2\cos\dfrac{x}{2}+2=0\)
b) \(8\cos^2x+2\sin x-7=0\)
c) \(2\tan^2c+3\tan x+1=0\)
d) \(\tan x-2\cos x+1=0\)
a) Đặt t = cos![]() , t ∈ [-1 ; 1] thì phương trình trở thành
, t ∈ [-1 ; 1] thì phương trình trở thành
(1 - t2) - 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ ![]()
Phương trình đã cho tương đương với
cos![]() = 1 ⇔
= 1 ⇔ ![]() = k2π ⇔ x = 4kπ, k ∈ Z.
= k2π ⇔ x = 4kπ, k ∈ Z.
b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành
8(1 - t2) + 2t - 7 = 0 ⇔ 8t2 - 2t - 1 = 0 ⇔ t ∈ {![]() }.
}.
Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :
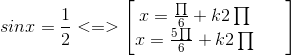
và ![]()
Đáp số : x = ![]() + k2π; x =
+ k2π; x = ![]() + k2π;
+ k2π;
x = arcsin(![]() ) + k2π; x = π - arcsin(
) + k2π; x = π - arcsin(![]() ) + k2π, k ∈ Z.
) + k2π, k ∈ Z.
c) Đặt t = tanx thì phương trình trở thành 2t2 + 3t + 1 = 0 ⇔ t ∈ {-1 ; ![]() }.
}.
Vậy ![]()
d) Đặt t = tanx thì phương trình trở thành
t - ![]() + 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
+ 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
Vậy ![]()
Giải pt sau:
A. (Sinx+1)(sinx-√2)=0
B.2sinxcosx=1
C. 4sinxcosxcos2x+1=0
D. Sin4x-cos4x=0
E. (Sinx+1)(2cos2x-√2)
F. Sin2x=cos4x/2-sin4x/2
d.
\(\Leftrightarrow\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)=0\)
\(\Leftrightarrow sin^2x-cos^2x=0\)
\(\Leftrightarrow-cos2x=0\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
e. Đề thiếu
f.
\(\Leftrightarrow sin2x=\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)\left(cos^2\frac{x}{2}+sin^2\frac{x}{2}\right)\)
\(\Leftrightarrow sin2x=cos^2\frac{x}{2}-sin^2\frac{x}{2}\)
\(\Leftrightarrow sin2x=cosx\)
\(\Leftrightarrow sin2x=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-x+k2\pi\\2x=x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
a.
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\sqrt{2}>1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=-\frac{\pi}{2}+k2\pi\)
b.
\(\Leftrightarrow sin2x=1\)
\(\Leftrightarrow2x=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
c.
\(\Leftrightarrow2sin2x.cos2x=-1\)
\(\Leftrightarrow sin4x=-1\)
\(\Leftrightarrow4x=-\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{\pi}{8}+\frac{k\pi}{2}\)