Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
0
Số lượng câu trả lời
146
Điểm GP
28
Điểm SP
116
Người theo dõi (3)
Đang theo dõi (0)
H24
H24
Câu trả lời:
Vợ chồng A Phủ 5.
H24
Câu trả lời:
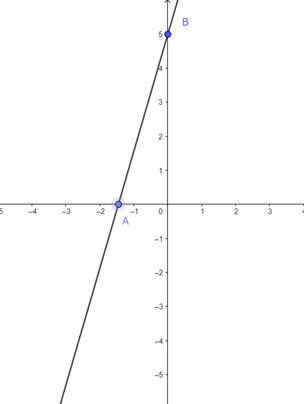
Tùng Trương Quang Mình vẽ bằng Geogebra đấy ạ:v
H24
Câu trả lời:
(m;-2) chắc thế ạ):
H24
Câu trả lời:
Thôi thấy thế vẽ luôn cho bạn vậy:D