Trên đường tròn ( O; 3cm) lấy bốn điểm A, B, C, D. Nối các điểm đó với nhau. Hỏi có bao nhiêu dây cung và bao nhiêu tam giác được tạo thành.?
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn. Đường tròn (O’) có vị trí tương đối nào với đường tròn (O) ?

Đường tròn (O’) tiếp xúc trong với đường tròn (O).
Đúng 0
Bình luận (0)
Câu 59: Trên hình bên, ta có đường tròn (O; R)A. Điểm O cách mọi điểm trên đường tròn một khoảng RB. Điểm O cách mọi điểm trên hình tròn một khoảng R O R C. Điểm O nằm trên đường tròn D. Chỉ có câu C đúngCâu 60: Gọi S1 là diện tích hình tròn bán kính R1 1 cmS2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:A. S2 2S1 B. S2 S1 C. S2 4S1 ...
Đọc tiếp
Câu 59: Trên hình bên, ta có đường tròn (O; R)
A. Điểm O cách mọi điểm trên đường tròn một khoảng R
B. Điểm O cách mọi điểm trên hình tròn một khoảng R
C. Điểm O nằm trên đường tròn
D. Chỉ có câu C đúng
Câu 60: Gọi S1 là diện tích hình tròn bán kính R1 = 1 cm
S2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:
A. S2 = 2S1 B. S2 = S1 C. S2 = 4S1 D. S2 = 3S1
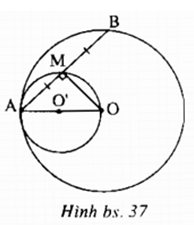
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn
a) Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O') ?
b) Đường tròn (O') có vị trí tương đối nào đối với đường tròn (O) ?
a: \(\widehat{AMO}=90^0\)
nên điểm M chuyển động trên đường tròn đường kính AO
b: Đường tròn (O') tiếp xúc trong với đường tròn (O)
Đúng 0
Bình luận (0)
Cho hai điểm phân biệt B và C cố định trên đường tròn tâm O bán kính O, điểm A di động trên đường tròn O. CMR khi A di động trên đường tròn O thì trực tâm của tam giác ABO di động trên một đường tròn.
Cho đường tròn (O) và 1 điểm P nằm bên trong đường tròn (P khác O). Gọi Q là 1 điểm tùy ý trên đường tròn (O). CMR khi điểm Q chuyển động trên đường tròn (O) thì giao điểm M các đường thẳng kẻ qua O vuông góc với PQ và tiếp tuyến kẻ từ Q của đường tròn (O) chạy trên 1 đường thẳng cố định
Cho đường tròn (O) và 1 điểm P nằm bên trong đường tròn (P khác O). Gọi Q là 1 điểm tùy ý trên đường tròn (O). CMR khi điểm Q chuyển động trên đường tròn (O) thì giao điểm M các đường thẳng kẻ qua O vuông góc với PQ và tiếp tuyến kẻ từ Q của đường tròn (O) chạy trên 1 đường thẳng cố định.
chiu
moi hoc lop 5 thui
doi toan lop 9 o dau ra
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn. Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O’).
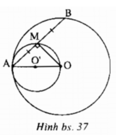
∠ (AMO) = 90 ° . Điểm M chuyển động trên đường tròn (O’) đường kính AO.
Đúng 0
Bình luận (0)
.a)Vẽ đường tròn (O;2cm)
b)Lấy điểm A bất kì trên đường tròn(O;2cm) vẽ đường tròn (A;2cm) đường tròn nay cắt đường tròn tâm O ở trên 2 điểm C,D
c)Vẽ đường tròn (C;2cm)
d)Chứng tỏ rằng đường tròn (C;2cm) đi qua 2 điểm O,A
Cho đường tròn (O), bán kính R 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Đọc tiếp
Cho đường tròn (O), bán kính R = 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.
b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?
c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)
Đúng 1
Bình luận (1)
Cho 2 đường tròn (O) và (O) cắt nhau tại A và B. Trên nửa mặt phẳng bờ là OO có chứa điểm A dựng tiếp tuyến CD chung của 2 đường tròn (C nằm trên đường tròn (O), D nằm trên đường tròn (O)). Dựng cát tuyến EBF song song với CD (E nằm trên đường tròn (O), F nằm trên đường tròn (O)). Kéo dài EC và FD cắt nhau tại điểm I.Gọi M và N lần lượt là giao điểm của AC và AD với EF. CMR: Tam giác MIN cân.
Đọc tiếp
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B. Trên nửa mặt phẳng bờ là OO' có chứa điểm A dựng tiếp tuyến CD chung của 2 đường tròn (C nằm trên đường tròn (O), D nằm trên đường tròn (O')). Dựng cát tuyến EBF song song với CD (E nằm trên đường tròn (O), F nằm trên đường tròn (O')). Kéo dài EC và FD cắt nhau tại điểm I.Gọi M và N lần lượt là giao điểm của AC và AD với EF. CMR: Tam giác MIN cân.