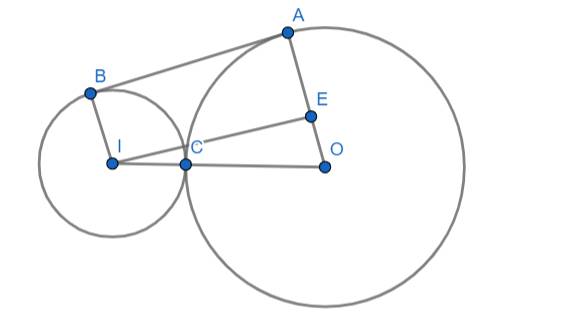
1) Cho (I;2cm) (O) đường kính 8cm tiếp xúp tại C, AB là tiếp tuyến của hai đường tròn. Tính tứ giác ABOI
2) Cho (O;3cm)(I;1cm) tiếp xúp tại C tiếp tuyến chung AB của hai đường tròn cắt OI tại M. Tính MC
3) Cho (O;12cm)(O'16cm) chát nhau tại A và B sao cho OA là tiếp tuyến của đường tròn (O'). Tính dây AB