Cho hàm số f ( x ) = sin 5 x 5 x k h i x ≠ 0 a + 2 k h i x = 0 . Tìm a để f(x) liên tục tại x=0
A.1
B. -1
C.-2
D.2
PB
Những câu hỏi liên quan
Cho hai hàm số y f(x) và y g(x) xác định trên R. Đặt S(x) f(x) + g(x) và P(x) f(x) g(x).Xét các mệnh đề:i) Nếu y f(x) và y g(x) là những hàm số chẵn thì y S(x) và y P(x) cũng là những hàm số chẵnii) Nếu y f(x) và y g(x) là những hàm số lẻ thì y S(x) là hàm số lẻ và y P(x) là hàm số chẵniii) Nếu y f(x) là hàm số chẵn, y g(x) là hàm số lẻ thì y P(x) là hàm số lẻSố mệnh đề đúng là: A. 1 B. 2 C. 3 D. Tất cả đều sai
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình vẽ
Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m sao cho hàm số y=f(x+m-3) nghịch biến trên khoảng (-2;4). Số phần tử của S là? biết m ϵ [-1;5)
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
MN
20 tháng 12 2020 lúc 22:58
Cho hàm số f(x) = sinx. Tính S = f'(x) + f''(x) + f'''(x) +...+ f(2019)(x)
\(f'\left(x\right)=cosx\)
\(f''\left(x\right)=-sinx\)
\(f^{\left(3\right)}\left(x\right)=-cosx\)
\(f^{\left(4\right)}\left(x\right)=sinx\)
Từ đó ta thấy được:
\(f^{\left(4k\right)}\left(x\right)=sinx\)
\(f^{\left(4k+1\right)}\left(x\right)=cosx\)
\(f^{\left(4k+2\right)}\left(x\right)=-sinx\)
\(f^{\left(4k+3\right)}\left(x\right)=-cosx\)
\(\Rightarrow f^{\left(4k\right)}\left(x\right)+f^{\left(4k+1\right)}\left(x\right)+f^{\left(4k+2\right)}\left(x\right)+f^{\left(4k+3\right)}\left(x\right)=0\)
\(\Rightarrow S=f^{\left(2017\right)}\left(x\right)+f^{\left(2018\right)}\left(x\right)+f^{\left(2019\right)}\left(x\right)\)
(Toàn bộ phần tổng đằng trước nhóm thành các cụm 4 số và triệt tiêu)
\(S=f^{\left(4.504+1\right)}\left(x\right)+f^{\left(4.504+2\right)}\left(x\right)+f^{\left(4.504+3\right)}\left(x\right)\)
\(=cosx-sinx-cosx=-cosx\)
Đúng 0
Bình luận (0)
Câu 35. Do cần tính giá trị \(g\left(1\right)\) nên chỉ cần xét khi \(x>0\)
Giả thiết\(\Rightarrow f'\left(x\right)-\dfrac{1}{2x}f\left(x\right)=-\dfrac{1}{2}-\dfrac{2}{x}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x}}.f'\left(x\right)-\dfrac{1}{2x\sqrt{x}}f\left(x\right)=-\dfrac{1}{2\sqrt{x}}-\dfrac{2}{x\sqrt{x}}\)
\(\Leftrightarrow\left[\dfrac{1}{\sqrt{x}}.f\left(x\right)\right]'=-\dfrac{1}{2\sqrt{x}}-\dfrac{2}{x\sqrt{x}}\)
\(\Rightarrow\dfrac{f\left(x\right)}{\sqrt{x}}=-\sqrt{x}+\dfrac{4}{\sqrt{x}}+C\)
Thay \(x=1\)
\(\Leftrightarrow\dfrac{5}{1}=-1+4+C\Rightarrow C=2\)
\(\Rightarrow f\left(x\right)=-x+4+2\sqrt{x}\)
Kì vậy ta, kết quả này thì \(g'\left(1\right)=\dfrac{1}{25}\) không có đáp án nào hết.
Mặc dù thay hàm \(f\left(x\right)\) vào điều kiện đề bài thỏa mãn
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho hàm số
f
(
x
)
ln
2019
-
ln
x
+
2
x
tính tổng
S
f
(
1
)
+
f
(
3
)
+
.
.
.
+
f
(...
Đọc tiếp
Cho hàm số f ( x ) = ln 2019 - ln x + 2 x tính tổng S = f ' ( 1 ) + f ' ( 3 ) + . . . + f ' ( 2019 )
A. 4305 2019
B. 2021
C. 2019 2021
D. 2020 2021
Cho hàm số f(x)3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
m
f
2
(
x
)
+
3
(
m
2
-
4
)
f
(
x
)
-
m
nghịch biến trên khoảng
(
0
;...
Đọc tiếp
Cho hàm số f(x)=3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 m f 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng ( 0 ; π 2 ) . Số tập con của S bằng
Cho hàm số
f
(
x
)
4
x
4
x
+
2
Tính tổng:
S
f
(
1
2017
)
+
f
(
2...
Đọc tiếp
Cho hàm số f ( x ) = 4 x 4 x + 2 Tính tổng:
S = f ( 1 2017 ) + f ( 2 2017 ) + . . . + f ( 2016 2017 )
A.S = 1007
B. S = 1009
C. S = 1008
D. S = 1006
Đáp án C
Chứng minh nhận xét: Nếu a + b = 1 thì 
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
ln
2018
x
x
+
1
Tính tổng
S
f
(
1
)
+
f
(
2
)
+
.
.
.
+
f
(
2018
)
A
.
...
Đọc tiếp
Cho hàm số f ( x ) = ln 2018 x x + 1 Tính tổng S = f ' ( 1 ) + f ' ( 2 ) + . . . + f ' ( 2018 )
A . S = 2018 2019
B . S = 1
C . S = ln 2018
D . S = 2018
Cho hàm số đa thức bậc ba yf(x) có đồ thị của các hàm số yf(x), yf (x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng A. 0 B. -6 C. -7 D. -5
Đọc tiếp
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
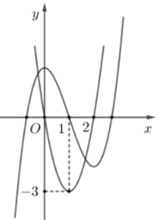
A. 0
B. -6
C. -7
D. -5
Ta có 
Quan sát đồ thị có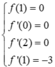 
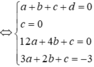
Đặt 
phương trình trở thành:
Khi đó 
Phương trình này có 3 nghiệm phân biệt
Tổng các phần tử củaS bằng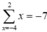 
Chọn đáp án C.
Đúng 0
Bình luận (0)