Cho hình chóp S.ABCD có S C = x 0 < x < a 3 , các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi x = a m n m , n ∈ ℕ * . Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
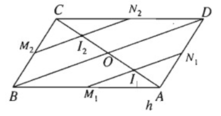
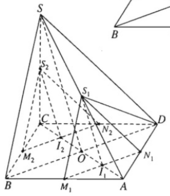
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI = x (0 < 0 < a). Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
a) Trường hợp 1 .
I thuộc đoạn AO (0 < x < a/2)
Khi đó I ở vị trí I1
Ta có: (α) // (SBD)
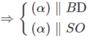
Vì (α) // BD nên (α) cắt (ABD) theo giao tuyến M1N1 ( qua I1) song song với BD
Tương tự (α) // SO nên (α) cắt (SOA) theo giao tuyến
S1T1 song song với SO.
Ta có thiết diện trong trường hợp này là tam giác S1M1N1.
Nhận xét. Dễ thấy rằng S 1 M 1 / / S B v à S 1 N 1 / / S D . Lúc đó tam giác S1M1N1 đều.
Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)
Khi đó I ở vị trí I2. Tương tự như trường hợp 1 ta có thiết diện là tam giác đều
S 2 M 2 N 2 c ó M 2 N 2 / / B D , S 2 M 2 / / S B , S 2 N 2 / / S D .
Trường hợp 3. I ≡ O. Thiết diện chính là tam giác đều SBD.
b) Ta lần lượt tìm diện tích thiết diện trong các trường hợp 1,2,3.
Trường hợp 1. I thuộc đoạn AO (0 < x < a/2)
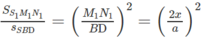
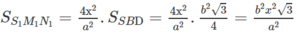
Trường hợp 2. I thuộc đoạn OC (a/2 < x < a)
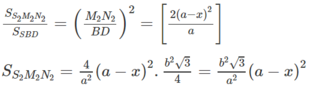
Trường hợp 3. I ≡ O.
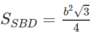
Tóm lại
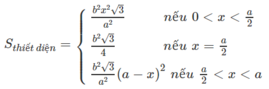
∗ Đồ thị của hàm số S theo biến x như sau:
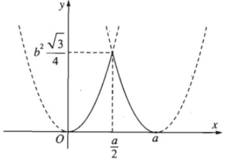
Vậy Sthiết diện lớn nhất khi và chỉ khi x = a/2.
Cho hình chóp S.ABCD, có đáy là hình bình hành, M và P là hai điểm lần lượt di động trên AD và SC sao cho: MA/MD = PS/PC = x (x>0). Mặt phẳng (a) đi qua M và song song với (SAB) cắt hình chóp S.ABCD theo thiết diện và cắt BD tại J.
a) Xác định x để PJ // (SAD)
b) Tính x để diện tích thiết diện bằng k lần diện tích tam giác SAB (k là số thực dương cho trước, \(k\le1\))
Bài này ko hề khó, đầu tiên ta dễ dàng xác định được thiết diện đi qua P theo Talet.
Gọi giao của thiết diện với BC, SD lần lượt là E, F
Để \(PJ||\left(SAD\right)\Rightarrow PJ||ME\Rightarrow PJME\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow PF=MJ\)
Đến đây sử dụng tỉ lệ tam giác đồng dạng là ra x
Câu b thì từ P kẻ vuông xuống ME và S vuông xuống AB, 2 đường cao này song song theo tỉ lệ tương ứng CP/CS (Talet). Vậy là ra tỉ lệ diện tích
Cho hình chóp S.ABCD có cạnh bên SA = a (0 <a < 3 )và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
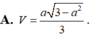
B. Đáp án khác.
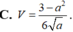
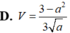
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0 < x < 1 . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S.ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức P = 1 − x 1 + x
A. 1/2
B. 1/5
C. 1/3
D. 3/5
Đáp án A

Kẻ M N ∥ B C N ∈ C D , N P ∥ S C P D , M Q ∥ S B Q ∈ S A
⇒ m p a cắt khối chóp S.ABCD theo thiết diện là MNPQ
Ta có M A A B = A Q S A = N D C D = x ⇒ S Q S A = S P S D = 1 − x (Định lý Thalet)
Mà Δ A M N = Δ A D N ⇒ V Q . A M N = V P . A D N = x V S . A M N = x 2 V S . A M N D = x 2 2 V
Và S N . A P Q = 1 3 d N ; S A D . S Δ A P Q = x 1 − x × V N . S A D = x 2 1 − x 2 V
Do đó V A Q M . D P N = V Q . A M N + V P . A N D + V N . A P Q = 3 x 2 − x 3 2 × V = 4 27 V
. ⇒ x 3 − 3 x 2 + 8 27 = 0 ⇒ x = 1 3 Vậy P = 1 − x 1 + x x = 1 3 = 1 2
Cho hình chóp S.ABCD có cạnh bên S A = ( 0 < α < 3 ) và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
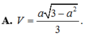
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O và AB = a, BC = a \(\sqrt{3}\)
(SAD) ⊥ (ABCD), SD tạo với đáy một góc 60◦ và ∆SAO cân tại S. Tính thể tích khối chóp S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt SAC là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a 3 . Tính thể tích khối chóp S.ABCD.
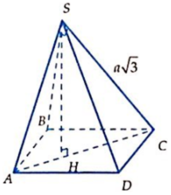
A. a 3 3 3
B. a 3 3 4
C. 2 a 3 3 3
D. a 3 3 6
Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a và tam giác ABC đều. Một điểm M thuộc cạnh BC sao cho BM= x ( 0< x< a), mặt phẳng (α) đi qua M song song với SA và SB. Biết rằng mp (α) cắt hình chóp theo 1 tứ giác. Tính diện tích thiết diện theo a và x
A. 3 4 a 2 - x 2
B. 3 2 a 2 - x 2
C. 2 4 a 2 - x 2
D. 1 4 a 2 - x 2
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a, AC = a 3 .
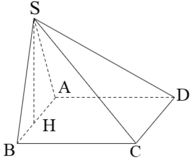
A. a 3
B. a 3 3 4
C. a 3 3 12
D. a 3 3